Zadanie 5.3.1.6
Kula uderza w przymocowany klocek
W górną krawędź prostopadłościanu o wymiarach \(l\times l\times 2l\) i masie \(\mu\) leżącego poziomo w polu sił ciężkości uderza kulka o masie \(m\) lecąca z prędkością \(v\). Przyjmując, że krawędź \(KK\) prostopadłościanu jest przymocowana do podłoża oraz, że zderzenie jest sprężyste, a kula odlatuje do tyłu, znajdź:
a) prędkość kątową, którą uzyskuje klocek w chwili zderzenia,
b) równanie ruchu klocka po zderzeniu.
a) prędkość kątową, którą uzyskuje klocek w chwili zderzenia,
b) równanie ruchu klocka po zderzeniu.
Wskazówka teoretyczna
Teoria - twierdzenie Steinera
Twierdzenie Steinera określa związek między momentami bezwładności względem dwóch równoległych osi oddalonych od siebie o \(d\) w sytuacji, gdy jedna z nich przechodzi przez środek masy bryły sztywnej:
gdzie \(m\) jest daną masą bryły sztywnej.
\(I=I_0+md^2\),
gdzie \(m\) jest daną masą bryły sztywnej.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- rozmiary prostopadłościanu \(l\times l\times 2l\),
- masa prostopadłościanu \(\mu\),
- masa kulki \(m\),
- prędkość kulki \(v\).
Szukane:
- prędkość kątowa klocka \(\varepsilon\),
- równanie ruchu klocka po zderzeniu.
Analiza sytuacji
Podczas zderzenia zachowany jest moment pędu układu kulka-klocek względem osi \(KK\).
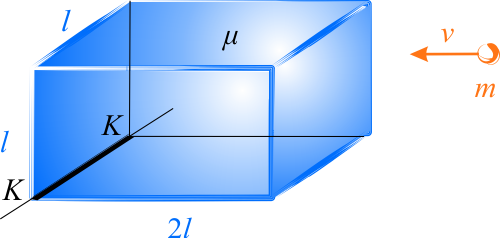
Moment pędu kulki \(mvl\) przed zderzeniem jest równy sumie momentu pędu kulki po zderzeniu \(-mul\) (zderzenie sprężyste) i momentu pędu klocka po zderzeniu
\(mvl=-mul+I\omega_0\),
gdzie \(u\) oznacza prędkość kulki po zderzeniu, \(\omega_0\) uzyskaną przez klocek prędkość kątową, a \(I\) jest jego momentem bezwładności względem osi \(KK\).
Punkt a)
Z równania \(mvl=-mul+I\omega_0\) wyznaczmy wartość \(u\)
\(\displaystyle{u=\frac{I\omega_0-mvl}{ml} }\)
Moment bezwładności prostopadłościanu względem osi równoległej do \(KK\) przechodzącej przez środek masy wynosi (zgodnie z rozwiązaniem zadania 5.2.1.4)
\(\displaystyle{I_0=\frac{1}{12}\mu(l^2+(2l)^2)=\frac{5}{12}\mu l^2 }\)
Zgodnie z twierdzeniem Steinera moment bezwładności \(I\) wynosi
\(I=I_0+\mu x^2\),
gdzie \(x\) jest odległością obu osi obrotu i jest równe połowie przekątnej prostokąta o bokach \(l\) i \(2l\).
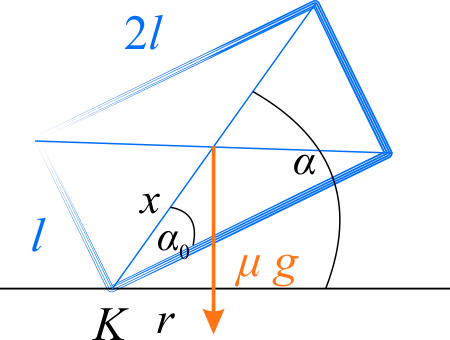
Z rysunku mamy
\(\displaystyle{x=\frac{1}{2}\sqrt{l^2+4l^2}=\frac{\sqrt{5}}{2}l }\)
i tak otrzymujemy
\(\displaystyle{I=\frac{5}{12}\mu l^2+\frac{5}{4}\mu l^2=\frac{5}{3}\mu l^2 }\)
Ponieważ zderzenie jest sprężyste, zachowana jest także energia kinetyczna. Energia kinetyczna kulki przed zderzeniem \(\displaystyle{\frac{mv^2}{2}}\) jest równa sumie energii kinetycznej kulki po zderzeniu \(\displaystyle{\frac{mu^2}{2}}\) i energii kinetycznej ruchu obrotowego klocka po zderzeniu \(\displaystyle{\frac{I\omega_0^2}{2}}\)
\(\displaystyle{\frac{1}{2}mv^2=\frac{1}{2}mu^2+\frac{1}{2}I\omega_o^2 }\)
Podstawiając teraz wyznaczoną wcześniej wartość \(u\), mamy:
\(\displaystyle{mv^2=m\left (\frac{I\omega_0-mvl}{ml}\right )^2+I\omega_o^2 }\)
\[\displaystyle{\frac{I^2\omega_0^2-2I\omega_0mvl+m^2v^2l^2}{ml^2}+I\omega_o^2-mv^2=0 }\] \[\displaystyle{\frac{I^2\omega_0^2}{ml^2}+I\omega_0^2-\frac{2Imvl}{ml^2}\omega_0+\frac{m^2v^2l^2}{ml^2}-mv^2=0 }\] \[\displaystyle{\left (\frac{I^2}{ml^2}+I\right )\omega_0^2-\frac{2Iv}{l}\omega_0+mv^2-mv^2=0 }\]
Otrzymujemy równanie kwadratowe postaci
\(\displaystyle{\left (\frac{I^2}{ml^2}+I\right )\omega_0^2-\frac{2Iv}{l}\omega_0=0 }\)
Równanie to ma dwa rozwiązania, z których \(\omega_0=0\) nie ma sensu fizycznego.
\(\displaystyle{\omega_0\left[ \left (\frac{I^2}{ml^2}+I\right )\omega_0-\frac{2Iv}{l}\right ]=0 }\)
Ostatecznie otrzymujemy więc
\(\displaystyle{\frac{I^2+Iml^2}{ml^2}\omega_0=\frac{2Iv}{l} }\)
\(\displaystyle{\omega_0=\frac{2Iv}{l}\cdot \frac{ml^2}{I^2+Iml^2}=\frac{2vml}{I+ml^2} }\)
Podstawiając jeszcze wartość \(\displaystyle{I=\frac{5}{3}\mu l^2 }\) otrzymujemy
\(\displaystyle{\omega_0=\frac{2vml}{\frac{5}{3}\mu l^2+ml^2} }\)
\(\displaystyle{\omega_0=\frac{2vm}{\frac{5}{3}\mu l+ml} }\)
Punkt b)
Oznaczmy przez \(\alpha\) kąt, jaki tworzy w dowolnej chwili przekątna bocznej ściany prostopadłościanu z podłożem.
W chwili początkowej \(t=0\) mamy dla kąta \(\alpha_0=\alpha(0)\) zależność
\(\displaystyle{\operatorname{tg}{\alpha_0}=\frac{l}{2l}=\frac{1}{2} }\),
a prędkość kątowa wynosi wtedy: \(\omega(0)=\omega_0\).
Ruch klocka po zderzeniu to ruch obrotowy, który można opisać drugą zasadą dynamiki dla ruchu obrotowego
\(M=\varepsilon I\),
gdzie \(\varepsilon\) jest przyspieszeniem kątowym zdefiniowanym jako
\(\displaystyle{\varepsilon=\frac{\mathrm{d}\omega }{\mathrm{d} t}=\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2} }\).
\(M\) jest wypadkowym momentem sił zewnętrznych działających na klocek. W naszym zadaniu \(M\) jest momentem siły ciężkości \(\mu g\) przyłożonej do środka masy i wynosi on:
\(M=\mu g r\),
gdzie \(r=x\cos\alpha\) jest ramieniem działania siły względem osi \(KK\). Zatem równanie ruchu ma postać:
\(\varepsilon I=M\)
\(\displaystyle{I\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}=\mu g\,r }\)
\(\displaystyle{I\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}-\mu g x\cos\alpha}\)
\(\displaystyle{I\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}-\mu g \frac{\sqrt{5}}{2}l\cos\alpha}\)
Odpowiedź
Prędkość kątową, którą uzyskuje klocek w chwili zderzenia opisuje zależność \(\displaystyle{\omega_0=\frac{2vm}{\frac{5}{3}\mu l+ml} }\), natomiast równanie ruchu klocka po zderzeniu ma postać \(\displaystyle{I\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}-\mu g \frac{\sqrt{5}}{2}l\cos\alpha}\).