Zadanie 5.3.2.1
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.2 Trening
  5. Zadanie 5.3.2.1

 Zadanie 5.3.2.1

Ciężarek i bęben
Do końca nici nawiniętej na bęben o promieniu \(10\,\mathrm{cm}\) przywiązano ciężar o masie \(0,5\,\mathrm{kg}\). Znajdź moment bezwładności bębna, jeżeli wiadomo, że ciężar porusza się w dół z przyspieszeniem \(\displaystyle{1\,\mathrm{\frac{m}{s^2}}}\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
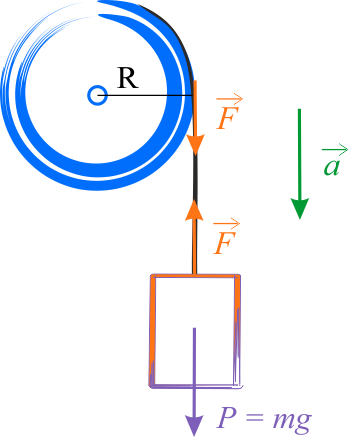
- promień bębna \(R=10\,\mathrm{cm}=0,1\,\mathrm{m}\),
- ciężar bębna \(0,5\,\mathrm{kg}\),
- przyspieszenie bębna \(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}} }\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- moment bezwładności bębna \(I\).

Odpowiedź

Moment bezwładności bębna wynosi \(\displaystyle{I=0,045\,\mathrm{kg\,m^2} }\).

Polecenie

Wyznacz moment bezwładności bębna. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(I=4,5\,\mathrm{kg\,m^2}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(I=0,45\,\mathrm{kg\,m^2}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(I=0,045\,\mathrm{kg\,m^2}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(I=0,0045\,\mathrm{kg\,m^2}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Rysunek


Zapiszmy drugą zasadę dynamiki dla ruchu postępowego odważnika

\(ma=P-F\)

oraz dla ruchu obrotowego bębna

\(I\varepsilon=FR\),

jak i związek pomiędzy tymi ruchami

\(a=\varepsilon R\)

Powyższe równania tworzą układ trzech równań, w którym mamy trzy niewiadome \(F\), \(\varepsilon\) i \(I\). Przekształcając te równania otrzymujemy:

\(\displaystyle{I=\frac{FR}{\varepsilon} }\)

\(F=mg-ma=m(g-a)\)

\(\displaystyle{\varepsilon=\frac{a}{R} }\)


Ostatecznie mamy

\(\displaystyle{I=\frac{m(g-a)R^2}{a} }\)

\(\displaystyle{I=\frac{0,5\cdot (10-1)0,1^2}{1} }\)

\(\displaystyle{I=0,045\,\mathrm{kg\,m^2} }\)




Odpowiedź

Moment bezwładności bębna wynosi \(\displaystyle{I=0,045\,\mathrm{kg\,m^2} }\).