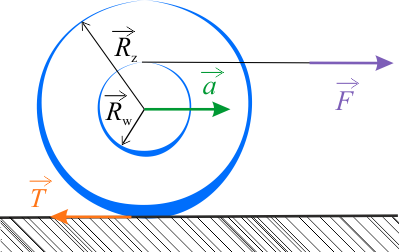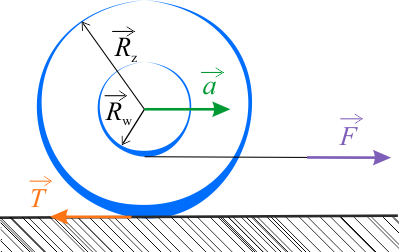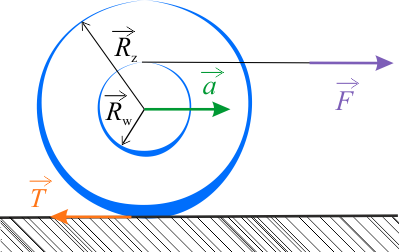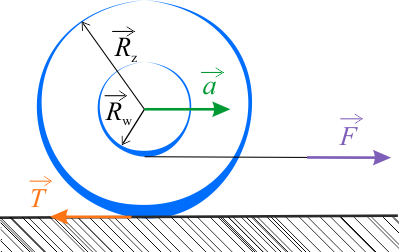Zadanie 5.3.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa szpuli \(m=18\,\mathrm{g}=0,018\,\mathrm{kg}\),
- moment bezwładności szpuli \(I=1,5\cdot 10^{-6}\,\mathrm{kg\,m^2}\),
- siła, z jaką ciągnięta jest szpula \(F=0,3\,\mathrm{N}\),
- promień zewnętrzny szpuli \(R_z=2,5\,\mathrm{cm}=0,025\,\mathrm{m}\),
- promień wewnętrzny szpuli \(R_w=1,5\,\mathrm{cm}=0,015\,\mathrm{m}\).
Szukane:
- przyspieszenie szpuli \(a\).
Odpowiedź
Szpula będzie poruszała się z różnym przyspieszeniem w zależności od tego, jak nawinięta jest nitka i jak leży szpula. W przypadku A przyspieszenie wynosi \(\displaystyle{a_A=2,63\,\mathrm{\frac{m}{s^2}} }\), w B: \(\displaystyle{a_B=0,65\,\mathrm{\frac{m}{s^2}} }\).
Polecenie
Wybierz rysunek, który poprawnie ilustruje treść zadania.
Od tego jednak, jaką sytuację wybierzemy, będzie zależał końcowy wynik zadania.
Polecenie
Zastanów się nad rozwiązaniem zadania. Wybierz układ równań, który można użyć w dwóch rozpatrywanych przypadkach zadania. Wybierz jeden prawidłowy, wśród dwóch przedstawionych poniżej.
\(\begin{eqnarray} \begin{cases} F-T=ma \\ \vec{R}_w\times\vec{F}+\vec{R}_z\times\vec{T}=I\vec{\varepsilon} \end{cases} \end{eqnarray} \)
\(\begin{eqnarray} \begin{cases} F+T=ma \\ R_wF+R_zT=I\varepsilon \end{cases} \end{eqnarray} \)
Rozwiązanie
Przyspieszenie liniowe \(a\) zależy od całkowitej siły, na którą składa się siła ciągnąca \(F\) oraz siła tarcia \(T\). Zgodnie z drugą zasadą dynamiki Newtona \(F_c=F-T=ma\). Nie znamy wartości siły tarcia, możemy ją jednak wyznaczyć z zasad dynamiki dla ruchu obrotowego, czyli \(\vec{M}=I\vec{\varepsilon}\) i licząc momenty obu działających sił
Polecenie
Zastanów się, jakie zwroty mają wielkości wektorowe, zapisane w powyższym układzie równań. Zapisz poprawne równania z rozdzieleniem na dwa analizowane przypadki (rysunek A i rysunek B). Wybierz prawidłowy zapis, wśród dwóch przedstawionych poniżej.
Przypadek B: \(-R_wF-R_zT=I\varepsilon\)
Przypadek B: \(-R_wF+R_zT=I\varepsilon\)
Rozwiązanie
Zakładając, że kierunek dodatni wektora przyspieszenia kątowego jest skierowany do kartki, możemy równanie
zapisać skalarnie w zależności od przypadku:
- przypadek A: \(R_wF+R_zT=I\varepsilon\)
- przypadek B: \(-R_wF+R_zT=I\varepsilon\)
Polecenie
Wyznacz wartości przyspieszenia liniowego \(a\). Wybierz jedną prawidłową wartość, spośród dwóch przedstawionych poniżej.
\(\displaystyle{a_A=2,63\,\mathrm{\frac{m}{s^2}} }\)
\(\displaystyle{a_B=0,65\,\mathrm{\frac{m}{s^2}} }\)
Rozwiązanie
Z wcześniejszych rozważań otrzymaliśmy dwa układy równań:
Przypadek A
Przypadek B
Jeśli dodatkowo skorzystamy z zależności przyspieszenia liniowego szpulki od przyspieszenia kątowego \(R_z\varepsilon=a\), pozostanie już tylko wykonanie kilku prostych przekształceń. Zajmijmy się najpierw przypadkiem pierwszym.
Podstawmy \(\displaystyle{\varepsilon=\frac{a_A}{R_z}}\) oraz podzielmy równanie drugie przez \(R_z\).
Po dodaniu stronami mamy
Przypadek B:
\[\begin{eqnarray} \begin{cases} F-T=ma_B \\ -\frac{R_w}{R_z}F+R_zT=I\frac{a_B}{R_z^2} \end{cases} \end{eqnarray} \] \[\displaystyle{\left (1-\frac{R_w}{R_z}\right )F=\left (m+\frac{I}{R_z^2}\right )a }\] \[\displaystyle{a_B=\frac{1-\frac{R_w}{R_z}}{m+\frac{I}{R_z^2}}F }\] \[\displaystyle{a_B=\frac{1-\frac{0,015}{0,025}}{0,018+\frac{1,5\cdot 10^{-6}}{0,025^2}}0,3 }\]
Odpowiedź
Szpula będzie poruszała się z różnym przyspieszeniem w zależności od tego, jak nawinięta jest nitka i jak leży szpula. W przypadku A przyspieszenie wynosi \(\displaystyle{a_A=2,63\,\mathrm{\frac{m}{s^2}} }\), w B \(\displaystyle{a_B=0,65\,\mathrm{\frac{m}{s^2}} }\).