Zadanie 5.3.2.3
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.2 Trening
  5. Zadanie 5.3.2.3

 Zadanie 5.3.2.3

Drabina przy ścianie
Przy ścianie stoi oparta o nią pod kątem \(70^{\circ}\) do poziomu drabina o masie \(15\,\mathrm{kg}\) i długości \(8\,\mathrm{m}\). Jak wysoko może na nią wejść człowiek o masie \(80\,\mathrm{kg}\), aby nie obawiać się zsunięcia? Współczynnik tarcia o podłogę wynosi \(0,2\). Pomiń siłę tarcia pomiędzy ścianą i drabiną.

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- kąt oparcia drabiny \(\alpha=70^{\circ}\),
- masa drabiny \(m=15\,\mathrm{kg}\),
- długość drabiny \(l=8\,\mathrm{m}\),
- masa człowieka \(M=80\,\mathrm{kg}\),
- współczynnik tarcia \(\mu =0,2\).

Szukane:
- wysokość, na jaką może wejść człowiek, aby nie obawiać się zsunięcia \(x\).

Odpowiedź

Wysokość, na jaką może wejść człowiek, aby nie obawiać się zsunięcia wynosi \(x=4,5\,\mathrm{m}\).

Polecenie

Wyznacz wysokość, na jaką może wejść człowiek, aby nie obawiać się zsunięcia. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(x=7,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(x=5,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(x=4,5\,\mathrm{m}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(x=2,5\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Warunkiem bezpiecznego wejścia na drabinę jest jej stabilność, toteż brak ruchu, czyli wartość przyspieszenia zarówno postępowego jak i kątowego.

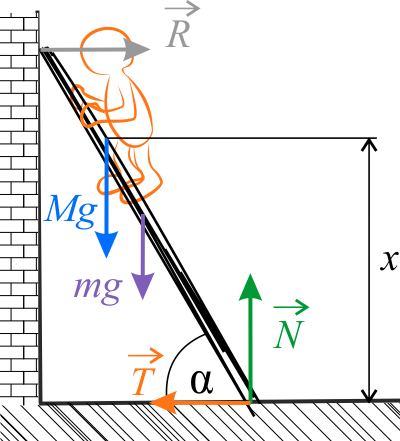
Rysunek


Na podstawie drugiej zasady dynamiki odpowiednio:
- dla ruchu postępowego \(m\vec{a}=0\),
- dla ruchu obrotowego \(I\vec{\varepsilon} =0\).

Dla sił można ten warunek rozpisać na składowe w kierunku równoległym do podłoża \(R-T=0\) oraz prostopadłym \(N-mg-Mg=0\). Podstawiając za \(T=\mu N\), otrzymujemy

\(R-\mu N=0\),

następnie podstawiamy za \(N\) wartość \(N=mg+Mg\) i mamy

\(R-\mu (m+M)g=0\)

\(R=\mu (m+M)g\)

Warunek dla momentów sił napiszemy po wyborze punktu odniesienia. Najlepiej jest wybrać punkt, w którym zaczepiona jest największa liczba sił, bądź siła, której wartość jest trudna do określenia. Proponuje punkt oparcia drabiny o podłogę, wówczas
\(\displaystyle{lR\sin\alpha-mg\frac{l}{2}\cos\alpha-Mgx\cos\alpha=0 }\)

Dzieląc obustronnie przez \(\cos\alpha\) i podstawiając wielkość \(R\), mamy

\(\displaystyle{l\mu (m+M)g \operatorname{tg}{\alpha}-mg\frac{l}{2}=Mgx }\)

\(\displaystyle{x=l\frac{\mu(m+M)\operatorname{tg}{\alpha}-\frac{1}{2} m}{M} }\)

\(\displaystyle{x=8\frac{0,2\,(15+80)\operatorname{tg}{70^{\circ}}-\frac{1}{2} 15}{80} }\)

\(x=4,5\,\mathrm{m}\)

Odpowiedź

Wysokość, na jaką może wejść człowiek, aby nie obawiać się zsunięcia wynosi \(x=4,5\,\mathrm{m}\).