Zadanie 5.3.2.4
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.3. Ruch obrotowy bryły sztywnej
  4. 5.3.2 Trening
  5. Zadanie 5.3.2.4

 Zadanie 5.3.2.4

Szpula ciągnięta siła pod kątem do podłoża
Ciężka szpula z nawiniętą nicią, do której przyłożono siłę \(\vec{F}\) leży na płaszczyźnie poziomej. W którą stronę i z jakim przyspieszeniem liniowym będzie poruszać się szpula w zależności od kąta między kierunkiem działania siły a płaszczyzną? Masa szpuli \(m\), zewnętrzny i wewnętrzny promień odpowiednio \(R\) i \(r\), moment bezwładności względem osi przechodzącej przez środek \(I_0\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Jeśli chcesz zobaczyć doświadczenie ze szpulą, uruchom kliknięciem link  nieposłuszna szpula

Dane i szukane

Dane:
- masa szpuli \(m\),
- zewnętrzny promień \(R\),
- wewnętrzny promień \(r\),
- moment bezwładności względem osi przechodzącej przez środek \(I_0\),
- przyłożona siła \(\vec{F}\).

Szukane:
- przyspieszenie liniowe \(a\),
- kierunek ruchu szpuli.

Odpowiedź

Przyspieszenie liniowe ma postać

\(\displaystyle{a=\frac{F(R\cos\alpha-r)R}{\left (I_0+mR^2\right )} }\)

Widać, że dla \(\displaystyle{\cos\alpha>\frac{r}{R}}\) szpula nawija się na nić, gdyż wtedy \(a>0\), dla \(\displaystyle{\cos\alpha<\frac{r}{R} }\), czyli dla \(a<0\) nić rozwija się ze szpuli, a dla \(\displaystyle{\cos\alpha=\frac{r}{R} }\) szpula spoczywa.

Polecenie

Wyznacz wartość przyspieszenia liniowego. Wybierz jedną prawidłową wartość, spośród dwóch przedstawionych poniżej.

Wybór 1 z 2

\(\displaystyle{a=\frac{F(R\cos\alpha-r)R}{I_0+mR^2} }\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\displaystyle{a=\frac{FR\cos\alpha-r}{I_0} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Załóżmy, że szpula nie ślizga się. Siła \(\vec{F}\) wywołuje obrót dookoła chwilowej osi \(A\)

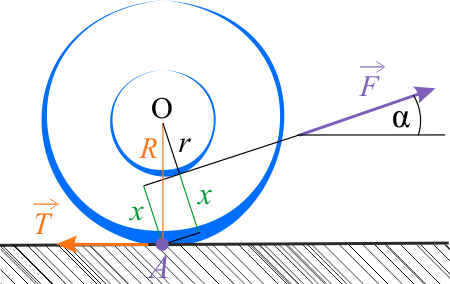
Rysunek


Ramię tej siły wynosi \(x\). Z rysunku widać, że

\(\displaystyle{\frac{r+x}{R}=\cos\alpha }\),

czyli
\(x=R\cos\alpha-r\)

Ramię siły tarcia \(T\) jest równe zeru, gdyż jest ona przyłożona do chwilowej osi obrotu \(A\). Zatem równanie tego ruchu ma postać

\(Fx=I_A\varepsilon\),

gdzie \(\displaystyle{\varepsilon=\frac{a}{R} }\). Jak wynika z twierdzenia Steinera, moment bezwładności szpuli względem osi \(A\) \(I_A\) można wyrazić za pomocą momentu bezwładności względem osi przechodzącej przez środek masy \(I_0\) oraz odległości \(R\) pomiędzy tymi osiami:

\(I_A=I_0+mR^2\)

Otrzymujemy równanie

\(\displaystyle{F(R\cos\alpha-r)=\frac{\left (I_0+mR^2\right )a}{R} }\),

a stąd przyspieszenie \(a\) wynosi

\(\displaystyle{a=\frac{F(R\cos\alpha-r)R}{\left (I_0+mR^2\right )} }\)

Odpowiedź

Przyspieszenie liniowe ma postać

\(\displaystyle{a=\frac{F(R\cos\alpha-r)R}{\left (I_0+mR^2\right )} }\)

Widać, że dla \(\displaystyle{\cos\alpha>\frac{r}{R}}\) szpula nawija się na nić, gdyż wtedy \(a>0\), dla \(\displaystyle{\cos\alpha<\frac{r}{R} }\), czyli dla \(a<0\) nić rozwija się ze szpuli, a dla \(\displaystyle{\cos\alpha=\frac{r}{R} }\) szpula spoczywa.