Rozwiązanie

Minimalną pracę przy przewracaniu klocka wykonamy wtedy, kiedy blok ma prędkość zero, czyli stoi na jednej ze swoich krawędzi. Inaczej mówiąc, energia kinetyczna bloku w momencie przechyłu, równa jest zeru.

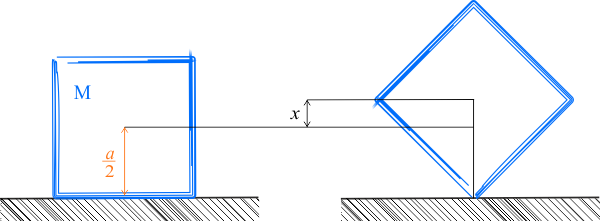
Ponieważ pole grawitacyjne jest polem zachowawczym, praca, jaką wykonujemy przy stawianiu bloku na krawędź, zostanie zużyta w całości na zwiększenie jego energii potencjalnej w tym polu. Nasz blok składa się z wielu cząsteczek i nad każdą z nich jest wykonywana praca. Jeżeli jednak, zgodnie z założeniem, nie nadaliśmy mu w momencie przechyłu dodatkowej energi kinetrycznej, to przy obliczaniu różnicy energii potencjalnej postępujemy tak, jak gdyby cała masa bloku była skupiona w jego środku masy. Środek masy zwiększył swoją wysokość o \(x\). Czyli zgodnie z rysunkiem mamy:


gdzie \(E_{p1}\), \(E_{p2}\) oznaczają odpowiednio energię potencjalną środka masy w położeniu początkowym i końcowym.

Oczywiście, gdy blok się przewróci, to zyskana wcześniej energia potencjalna zmieni się na energię kinetyczną ruchu obrotowego względem jego krawędzi, a ta z kolei, przy zderzeniu bloku o ziemię, na ciepło.