Zadanie 5.4.1.1
  1. Kurs obliczeniowy z fizyki
  2. 5. Dynamika układu punktów
  3. 5.4. Zasady zachowania w ruchu obrotowym.
  4. 5.4.1 Nauka
  5. Zadanie 5.4.1.1

 Zadanie 5.4.1.1

Złączenie dwóch tarcz
Dwie poziome tarcze wirują wokół pionowej osi przechodzącej przez ich środek. Momenty bezwładności tarcz wynoszą \(I_1\), \(I_2\), a ich prędkości kątowe \(\omega_1\) i \(\omega_2\). Po upadku tarczy górnej na dolną obie tarcze (w wyniku działania siły tarcia) obracają się dalej jak jedno ciało. Wyznacz
a) prędkość kątową tarcz po złączeniu;
b) pracę wykonaną przez siły tarcia.

 Wskazówka teoretyczna

 Teoria - zasada zachowania momentu pędu
Zasada zachowania momentu pędu

\(\displaystyle{\sum_{i=1}^N\vec{L}_i=\sum_{j=1}^N\vec{L}_j }\)

Suma momentów pędu ciała przed zderzeniem, połączeniem lub rozpadem równa jest sumie momentów pędu ciał po zderzeniu, połączeniu lub rozpadzie.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Jeśli chcesz zobaczyć doświadczenie, uruchom kliknięciem link  zachowanie momentu pędu

Dane i szukane

Dane:
- moment bezwładności tarczy pierwszej \(I_1\),
- moment bezwładności tarczy drugiej \(I_2\),
- prędkość kątowa tarczy pierwszej \(\omega_1\),
- prędkość kątowa tarczy drugiej \(\omega_2\).

Szukane:
- prędkość kątowa tarcz po złączeniu \(\omega\)
- praca wykonana przez siły tarcia \(W\).

Analiza sytuacji

Na rysunku przedstawiono obie tarcze przed i po upadku tarczy górnej na dolną.

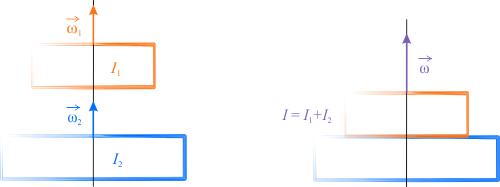
Rysunek


Wyrównanie się prędkości kątowych obu tarcz następuje pod wpływem sił tarcia, dlatego też nie możemy skorzystać z zasady zachowania energii kinetycznej ruchu obrotowego, gdyż pewna jej część zmienia się na energię cieplną. Możemy natomiast skorzystać z zasady zachowania momentu pędu, ponieważ na układ nie działa żaden zewnętrzny moment sił.

Punkt a)

Momenty pędu mają kierunek prędkości kątowych, ponieważ obrót następuje wokół osi symetrii, dlatego też możemy pominąć oznaczenia wektorowe. Moment pędu układu \(L_1\) przed połączeniem się tarcz wynosi

\(L_1=I_1\omega_1+I_2\omega_2\),

natomiast po połączeniu moment pędu \(L_2\) wynosi

\(L_2=(I_1+I_2)\omega\)

W powyższym wzorze \(\omega\) jest prędkością układu dwóch tarcz po połączeniu.

Z zasady zachowania momentu pędu \(L_1=L_2\), toteż porównując oba powyższe wzory otrzymujemy wyrażenie

\(I_1\omega_1+I_2\omega_2=(I_1+I_2)\omega\)

\(\displaystyle{\omega=\frac{I_1\omega_1+I_2\omega_2}{I_1+I_2} }\)

Punkt b)

Pracę, która została wykonana przez siły tarcia podczas wyrównywania się prędkości tarcz (praca ta wydzieliła się w postaci ciepła powodując ogrzanie się tarcz), obliczamy jako różnicę energii kinetycznych układu początkowego i końcowego.

Na początku mieliśmy dwie tarcze:

\(\displaystyle{E_{k1}=\frac{I_1\omega_1^2}{2}+\frac{I_2\omega_2^2}{2} }\)

Na końcu dwie tarcze połączyły się wirując razem

\(\displaystyle{E_{k2}=\frac{(I_1+I_2)\omega^2}{2} }\)

Prędkość kątową \(\omega\), obliczoną w poprzednim etapie rozwiązania, wstawiamy do wyrażenia \(E_{k2}\) i liczymy różnicę energii:
\(\displaystyle{W=E_{k2}-E_{k1} }\)

\(\displaystyle{W=-\frac{I_1\omega_1^2}{2}-\frac{I_2\omega_2^2}{2}+\frac{(I_1+I_2)}{2} \left (\frac{I_1\omega_1+I_2\omega_2}{I_1+I_2}\right )^2 }\)

\(\displaystyle{W=-\frac{I_1I_2(\omega_1-\omega_2)^2}{2(I_1+I_2)} }\)

Warto zauważyć, że dla \(\omega_1=\omega_2\) praca wyniesie zero.

\(\displaystyle{W=-\frac{I_1\omega_1^2+I_2\omega_2^2}{2}+\frac{1}{2}\frac{I_1^2\omega_1^2+2I_1I_2\omega_1\omega_2+I_2^2\omega_2^2}{I_1+I_2} }\)

\(\displaystyle{W=-\frac{(I_1\omega_1^2+I_2\omega_2^2)(I_1+I_2)}{2(I_1+I_2)}+\frac{I_1^2\omega_1^2+2I_1I_2\omega_1\omega_2+I_2^2\omega_2^2}{2(I_1+I_2)} }\)

\(\displaystyle{W=-\frac{I_1^2\omega_1^2+I_1I_2\omega_1^2+I_1I_2\omega_2^2+I_2^2\omega_2^2}{2(I_1+I_2)}+\frac{I_1^2\omega_1^2+2I_1I_2\omega_1\omega_2+I_2^2\omega_2^2}{2(I_1+I_2)} }\)

\(\displaystyle{W=-\frac{I_1I_2\omega_1^2+I_1I_2\omega_2^2-2I_1I_2\omega_1\omega_2}{2(I_1+I_2)} }\)

\(\displaystyle{W=-\frac{I_1I_2(\omega_1^2-2\omega_1\omega_2+\omega_2^2)}{2(I_1+I_2)} }\)

\(\displaystyle{W=-\frac{I_1I_2(\omega_1-\omega_2)^2}{2(I_1+I_2)} }\)

Odpowiedź

Prędkość kątowa tarcz po złączeniu wynosi \(\displaystyle{\omega=\frac{I_1\omega_1+I_2\omega_2}{I_1+I_2} }\), natomiast praca wykonana przez siły tarcia wynosi \(\displaystyle{W=-\frac{I_1I_2(\omega_1-\omega_2)^2}{2(I_1+I_2)} }\).