Zadanie 5.4.1.2
Toczący się walec w walcu
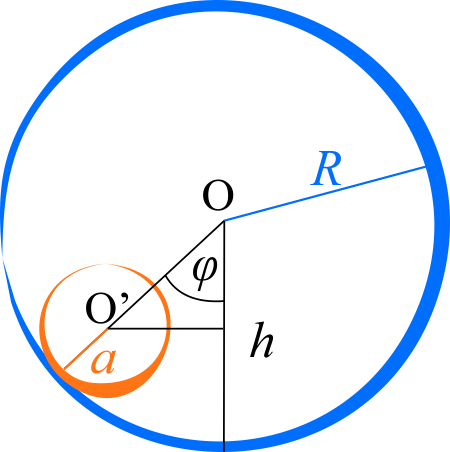
Jednorodny walec o masie \(m\) i promieniu \(a\) toczy się w polu ciężkości wewnątrz walca o promieniu \(R\). Znajdź równanie ruchu walca wychylonego w chwili początkowej z położenia równowagi o kąt \(\varphi_0\).
Wskazówka teoretyczna
Teoria - twierdzenie Steinera
Twierdzenie Steinera określa związek między momentami bezwładności względem dwóch równoległych osi oddalonych od siebie o \(d\) w sytuacji, gdy jedna z nich przechodzi przez środek masy bryły sztywnej:
gdzie \(m\) jest daną masą bryły sztywnej.
\(I=I_0+md^2\),
gdzie \(m\) jest daną masą bryły sztywnej.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa wewnętrznego walca \(m\),
- promień wewnętrznego walca \(a\),
- promień zewnętrznego walca \(R\),
- wychylenie walca w chwili początkowej \(\varphi_0\).
Szukane:
- równanie ruchu małego walca.
Analiza sytuacji
Środek małego walca porusza się wewnątrz dużego walca po torze będącym wycinkiem okręgu o promieniu \(R-a\) z chwilową prędkością kątową \(\displaystyle{\omega_1=\frac{\mathrm{d}\varphi }{\mathrm{d} t} }\), a zatem z prędkością liniową
\(\displaystyle{v=\omega_1(R-a)=\frac{\mathrm{d}\varphi }{\mathrm{d} t}(R-a) }\)
Prędkość kątowa obrotu małego walca wokół osi przechodzącej przez jego środek \(O'\) wynosi więc
\(\displaystyle{\omega_2=\frac{v}{a}=\frac{\mathrm{d}\varphi }{\mathrm{d} t}\frac{R-a}{a} }\)
Skorzystamy z zasady zachowania energii. Całkowita energia kinetyczna małego walca to suma energii kinetycznej ruchu obrotowego względem osi przechodzącej przez środek \(O\) dużego walca i energii kinetycznej ruchu obrotowego względem osi przechodzącej przez jego środek \(O'\). Zatem
\(\displaystyle{E_k=\frac{I\omega_1^2}{2}+\frac{I_0\omega_2^2}{2} }\),
gdzie \(\displaystyle{I_0=\frac{ma^2}{2} }\) jest momentem bezwładności małego walca względem osi przechodzącej przez punkt \(O'\), a \(I\) jest jego momentem bezwładności względem osi przechodzącej przez punkt \(O\). Zgodnie z twierdzeniem Steinera:
\(I=I_0+m(R-a)^2\).
Rozwiązanie
Całkowita energia kinetyczna małego walca wychylonego o kąt \(\varphi\) od położenia równowagi wynosi zatem
\(\displaystyle{E_k=\frac{1}{2}\left (\frac{ma^2}{2}+m(R-a)^2\right ) \left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2+\frac{1}{2}\frac{ma^2}{2}\frac{(R-a)^2}{a^2}\left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2 }\)
\[\displaystyle{E_k=\left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2m\left (\frac{a^2}{4}+\frac{1}{2}(R-a)^2 +\frac{a^2}{4}\frac{(R-a)^2}{a^2}\right ) }\] \[\displaystyle{E_k=\frac{1}{4}\left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2m\left (a^2+2(R-a)^2+(R-a)^2\right ) }\]
\(\displaystyle{E_k=\frac{3}{4}m\left (\frac{\mathrm{d}\varphi }{\mathrm{d} t}\right )^2\left ((R-a)^2+\frac{1}{3}a^2\right ) }\)
Energia potencjalna w tym samym momencie wynosi \(E_p=mg(h-a)\). Z wcześniejszego rysunku widać, że
\(\displaystyle{\frac{R-h}{R-a}=\cos\varphi }\),
a stąd mamy
\(h=R(1-\cos\varphi)+a\cos\varphi\).
Zatem
\[E_p=mg(R-R\cos\varphi+a\cos\varphi-a)\] \[E_p=mg(R(1-\cos\varphi)-a(1-\cos\varphi))\]
\(E_p=mg(R-a)(1-\cos\varphi)\)
Ponieważ suma \(E_k+E_p\), zgodnie z zasadą zachowania energii mechanicznej, jest stała, więc
\(\displaystyle{\frac{\mathrm{d} }{\mathrm{d} t}(E_k+E_p)=0}\).
Obliczamy pochodne:
\(\displaystyle{\frac{\mathrm{d}E_k }{\mathrm{d} t}=\frac{3}{2}m \frac{\mathrm{d}\varphi }{\mathrm{d} t} \frac{\mathrm{d}^2\varphi }{\mathrm{d} t^2} \left [(R-a)^2+\frac{1}{3}a^2\right ] }\)
\(\displaystyle{\frac{\mathrm{d}E_p }{\mathrm{d} t}=mg(R-a)\sin\varphi\frac{\mathrm{d}\varphi }{\mathrm{d} t} }\)
Teraz otrzymujemy równanie ruchu
\(\displaystyle{\frac{3}{2} \left [(R-a)^2+\frac{1}{3}a^2\right ]\frac{\mathrm{d}^2\varphi }{\mathrm{d} t^2}+g(R-a)\sin\varphi=0 }\)
Odpowiedź
Równanie ruchu walca wychylonego w chwili początkowej z położenia równowagi ma postać \(\displaystyle{\frac{3}{2} \left [(R-a)^2+\frac{1}{3}a^2\right ]\frac{\mathrm{d}^2\varphi }{\mathrm{d} t^2}+g(R-a)\sin\varphi=0 }\).