Zadanie 6.1.1.6
Ruch punktu materialnego
Ruch punktu materialnego jest opisany równaniami parametrycznymi \(x=a \cos^2(bt)\), \(y=a \sin^2(bt)\), gdzie \(a\) i \(b\) są wielkościami stałymi. Wyznacz tor ruchu oraz jego równanie jako funkcję czasu.
Wskazówka teoretyczna
Teoria - tor i równanie ruchu
Tor ruchu (trajektoria) – krzywa zakreślana w przestrzeni przez poruszające się ciało.
Jeżeli znamy współrzędne \(x\) i \(y\) poruszającego się ciała możemy wyznaczyć składowe wektora prędkości
\(\displaystyle{v_x=\frac{\mathrm{d}x }{\mathrm{d} t} }\) oraz \(\displaystyle{v_y=\frac{\mathrm{d}y }{\mathrm{d} t} }\),
jak i bezwzględną wartość prędkości
\(v=\sqrt{v_x^2+v_y^2}\)
Prędkość z przebytą drogą związana jest zależnością:
\(\displaystyle{v=\frac{\mathrm{d}s }{\mathrm{d} t} }\)
Z powyższej zależności możemy wyznaczyć równanie ruchu \(s(t)\) (rozwiązanie równania różniczkowego).
Jeżeli znamy współrzędne \(x\) i \(y\) poruszającego się ciała możemy wyznaczyć składowe wektora prędkości
jak i bezwzględną wartość prędkości
Prędkość z przebytą drogą związana jest zależnością:
Z powyższej zależności możemy wyznaczyć równanie ruchu \(s(t)\) (rozwiązanie równania różniczkowego).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- równania opisujące ruch punktu materialnego \(x=a \cos^2(bt)\), \(y=a \sin^2(bt)\),
Szukane:
- tor ruchu,
- równanie ruchu w funkcji czasu \(s(t)\).
Wyznaczenie toru ruchu
W celu znalezienia toru ruchu przeanalizujmy ruch punktu na podstawie podanych równań
\(x=a \cos^2(bt)\) oraz \(y=a \sin^2(bt)\)
Po dodaniu obu równań stronami, otrzymujemy:
\(x+y=a(\cos^2(bt)+\sin^2(bt))\)
\(x+y=a\cdot 1\)
\(y=-x+a\)
Otrzymane równanie przedstawia linię prostą. Jest to tor ruchu.
W obydwu równaniach występują funkcje trygonometryczne podniesione do kwadratu. Zbiór wartości funkcji \(f(x)=\sin^2 x\) jak i funkcji \(f(x)=\cos^2 x\) zawiera się w przedziale \(<0,1>\). Wartości maksymalne obu równań przyjmują wartość \(a\), a minimalna wartość to \(0\).
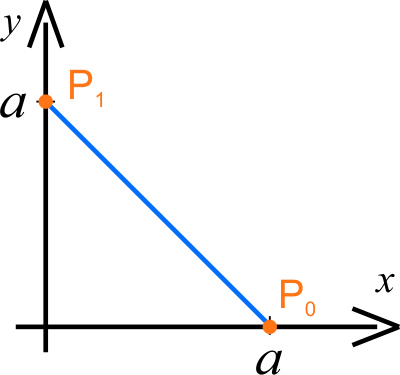
W chwili \(t=0\), mamy \(x_0=a\), \(y_0=0\), zatem punkt materialny w tej chwili znajduje się w punkcie \(P_0\). W chwili \(\displaystyle{t_1=\frac{\pi}{2b} }\), mamy \(x_1=0\), \(y_1=a\), czyli punkt materialny znajduje się w punkcie \(P_1\). W chwili \(\displaystyle{t_2=2t_1=\frac{\pi}{b} }\), mamy \(x_2=a\), \(y_2=0\). Wynika stąd, że punkt materialny wraca do położenia \(P_0\) i cały ruch się powtarza. Punkt materialny wykonuje więc ruch harmoniczny na odcinku \(P_0 P_1\) o okresie
\(\displaystyle{T=\frac{\pi}{b} }\)
Wyznaczenie równania ruchu
Współrzędne prędkości punktu otrzymujemy różniczkując równania parametryczne ruchu
\(\displaystyle{v_x=\frac{\mathrm{d}x }{\mathrm{d} t}=\frac{\mathrm{d} }{\mathrm{d} t}a \cos^2 (bt) }\)
\(\displaystyle{v_x=-2ab\cos(bt)\sin(bt)=-ab\sin(2bt) }\)
\(\displaystyle{v_y=\frac{\mathrm{d}y }{\mathrm{d} t}=\frac{\mathrm{d} }{\mathrm{d} t}a \sin^2 (bt) }\)
\(\displaystyle{v_y=2ab\sin(bt)\cos(bt)=ab\sin(2bt) }\)
Bezwzględną wartość prędkości obliczamy ze wzoru:
\(v=\sqrt{v_x^2+v_y^2}\)
\[v=\sqrt{(-ab\sin(2bt))^2+(ab\sin(2bt))^2 }\] \[v=ab\sqrt{2\sin^2(2bt) }\]
\(v=ab\sqrt{2 }\sin(2bt)\)
Gdy symbolem \(s\) oznaczymy odległość punktu materialnego od punktu \(P_0\), w którym punkt materialny znajdował się w chwili \(t=0\), będziemy mieli
\(\displaystyle{v=\frac{\mathrm{d}s }{\mathrm{d} t}=ab\sqrt{2 }\sin(2bt) }\)
\(\displaystyle{s=\int \sqrt{2}ab\sin(2bt)\mathrm{d}t }\)
\(\displaystyle{s=-\sqrt{2}ab\cdot \frac{1}{2b}\cos(2bt)+C }\)
\(\displaystyle{s=-\frac{a\sqrt{2}}{2}\cos(2bt)+C}\)
Wartość stałej \(C\) obliczamy z warunków początkowych: dla \(t=0\), \(s=0\)
\(\displaystyle{0=-\frac{a\sqrt{2}}{2}\cos(0)+C}\)
\(\displaystyle{C=\frac{a\sqrt{2}}{2} }\)
Ostatecznie otrzymujemy równanie ruchu
\(\displaystyle{s(t)=\frac{a\sqrt{2}}{2}\left [ 1-\cos(2bt)\right ] }\)
\(\displaystyle{s(t)=\frac{a\sqrt{2}}{2}\left [ 1-(1-2\sin^2(bt))\right ] }\)
\(\displaystyle{s(t)=a\sqrt{2}\sin^2(bt) }\)
Odpowiedź
Tor ruchu jest linią prostą. Równanie opisujące ruch punktu materialnego ma postać \(\displaystyle{s(t)=a\sqrt{2}\sin^2(bt) }\).
