Zadanie 6.1.1.5
  1. Kurs obliczeniowy z fizyki
  2. 6. Drgania i fale
  3. 6.1. Drgania swobodne.
  4. 6.1.1. Nauka
  5. Zadanie 6.1.1.5

 Zadanie 6.1.1.5

Kulka na sprężynie
Małą kulę o masie \(0,3\,\mathrm{ kg}\) podwieszono do sprężyny, która pod wpływem zawieszenia na niej masy \(0,049\,\mathrm{ kg}\) wydłużyła się o \(0,01\,\mathrm{m}\). Jaki jest okres drgań kulki?

 Wskazówka teoretyczna

 Teoria - siła sprężystości
Siła w ruchu harmonicznym ma postać:

\(F=ma=-m\omega^2 x=-kx\)

gdzie \(k=m\omega^2\) jest współczynnikiem proporcjonalności między siłą a wychyleniem z położenia równowagi. Siła w ruchu harmonicznym jest więc proporcjonalna do wychylenia, a kierunek jej wektora jest przeciwny do wychylenia.

Okres drgań ciężarka zawieszonego na sprężynie wynosi

\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}} }\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa kulki \(m=0,3\,\mathrm{ kg}\),
- masa zawieszonego ciała \(M=0,049\,\mathrm{ kg}\),
- wydłużenie sprężyny \(x=0,01\,\mathrm{m}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).

Szukane:
- okres drgań kulki \(T\).

Analiza sytuacji

Po zawieszeniu ciała o masie \(M\), sprężyna wydłuży się o \(x\) i masa \(M\) osiągnie stan równowagi, w którym równoważą się dwie siły: ciężkości i rozciągniętej sprężyny.

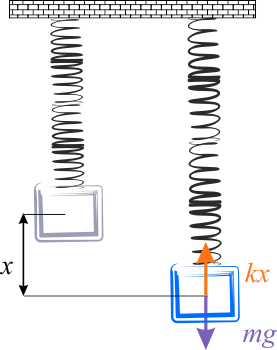
Rysunek

Znajomość wartości wydłużenia sprężyny pozwala na wyznaczenie stałej sprężystości. Ze stanu równowagi otrzymujemy:

\(Mg=kx\)

\(\displaystyle{k=\frac{Mg}{x} }\)


Znając współczynnik \(k\) możemy wyznaczyć okres drgań ciężarka.

Obliczenia

\(\displaystyle{k=\frac{Mg}{x}=\frac{0,049\cdot 10}{0,01}=49\,\mathrm{\frac{N}{m}} }\) \(\displaystyle{\left [\mathrm{\frac{kg\cdot \frac{N}{Kg} }{m}=\frac{N}{m}}\right ] }\)

\(\displaystyle{T=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{0,3}{49}}\approx 0,49\,\mathrm{s} }\)

Odpowiedź

Okres drgań kulki wynosi \(\displaystyle{T\approx 0,49\,\mathrm{s} }\).