Zadanie 6.3.1.1
Drgania słupa wody
W rurce o przekroju \(S\) zgiętej w kształcie litery U znajduje się słup wody o długości \(l\), przy czym w chwili początkowej poziom wody w jednym ramieniu rurki jest wyższy niż w drugim. Jaki będzie okres drgań słupa wody (pomijając siły lepkości)?
Wskazówka teoretyczna
Teoria - ocsylator harmoniczny
Oscylator harmoniczny jest to układ drgający, poddany działaniu sił sprężystych tj. sił proporcjonalnych do przemieszczenia \(x\) układu od położenia równowagi.
Równanie ruchu oscylatora harmonicznego otrzymujemy z II zasady dynamiki Newtona. Porównując dwie siły \(F_{wyp}=ma\) oraz \(F_{wyp}=-kx\), otrzymujemy
lub, po podstawieniu wielkości \(\displaystyle{\omega=\sqrt{\frac{k}{m}} }\)
Równanie ruchu oscylatora harmonicznego otrzymujemy z II zasady dynamiki Newtona. Porównując dwie siły \(F_{wyp}=ma\) oraz \(F_{wyp}=-kx\), otrzymujemy
\(\displaystyle{m\frac{\mathrm{d}^2x }{\mathrm{d} t^2}+kx=0 }\)
lub, po podstawieniu wielkości \(\displaystyle{\omega=\sqrt{\frac{k}{m}} }\)
\(\displaystyle{\frac{\mathrm{d}^2x }{\mathrm{d} t^2}+\omega^2 x=0 }\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- przekrój rurki \(S\),
- długość słupa wody \(l\).
Szukane:
- okres drgań słupa wody \(T\).
Analiza sytuacji
Załóżmy, że gęstość wody wynosi \(\rho\). Masa słupa wody o długości \(l\) i przekroju \(S\) wynosi zatem \(m=\rho l S\).
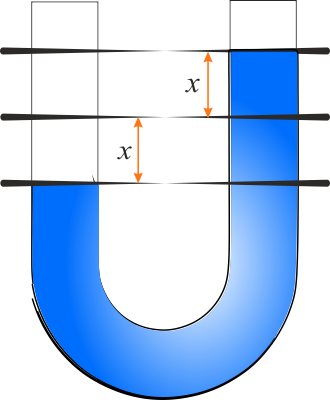
Oznaczmy przez \(x\) dowolne wychylenie poziomu wody z położenia równowagi w jednym z ramion rurki. Niezrównoważony słup wody ma zatem wysokość \(2x\), ponieważ jeśli w jednym ramieniu poziom wody jest o \(x\) wyżej od położenia równowagi, to w drugim ramieniu jest o \(x\) poniżej położenia równowagi.
Ciężar niezrównoważonego słupa wody o wysokość \(2x\) i przekroju \(S\) jest funkcją \(x\) i wynosi
\(F(x)=-mg=-\rho Vg=-2xS\rho g\)
Znak minus oznacza, że siła \(F\) jest skierowana przeciwnie do wychylenia \(x\), czyli w dół. Widać, że siła \(F\) jest do tego wychylenia proporcjonalna.
Zależność \(F(x) = -kx\), gdzie \(k=2S\rho g\)
Z drugiej zasady dynamiki wynika, że \(F=ma\), gdzie \(m\) jest masą całego słupa wody \(m=\rho lS\).
Otrzymujemy \(ma=-kx\)
\(\rho lSa=-2S\rho gx\)
Rozwiązanie
Przyspieszenie możemy zastąpić drugą pochodną wychylenia \(x\) po czasie
\(\displaystyle{\rho lS\frac{\mathrm{d}^2 x}{\mathrm{d} t^2} =-2S\rho gx }\)
\(\displaystyle{\frac{\mathrm{d}^2 x}{\mathrm{d} t^2} =-\frac{2 g}{l}x }\)
\(\displaystyle{\frac{\mathrm{d}^2 x}{\mathrm{d} t^2} +\frac{2 g}{l}x=0 }\)
Równanie to ma postać równania ruchu oscylatora harmonicznego\(\displaystyle{\frac{\mathrm{d}^2 x}{\mathrm{d} t^2} +\omega^2 x=0 }\),
gdzie \(\omega\) jest częstością drgań. po porównaniu obu równań, można stwierdzić, że \(\displaystyle{\omega=\sqrt{\frac{2g}{l} } }\)
Okres drgań jest więc równy
\(\displaystyle{T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{l}{2g}} }\)
Odpowiedź
Okres drgań słupa wody wynosi \(\displaystyle{T=2\pi \sqrt{\frac{l}{2g}} }\)
