Zadanie 6.3.1.6
Wahadło matematyczne na karuzeli
Ile wynosi okres drgań wahadła matematycznego o długości \(l\) wiszącego w odległości \(R\) od środka poziomej platformy karuzeli obracającej się ze stałą prędkością kątową \(\omega\)?
Wskazówka teoretyczna
Teoria - wahadło matematyczne
Wahadło matematyczne to punkt materialny o masie \(m\) zawieszony na nieważkiej nierozciągliwej nici o długości \(l\).
Równanie różniczkowe ruchu wahadła otrzymujemy z II zasady dynamiki ruchu obrotowego \(I\varepsilon=M\), gdzie \(I=ml^2\) jest momentem bezwładności punktu materialnego o masie \(m\) względem osi obrotu, a \(\displaystyle{\varepsilon=\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}}\) jest przyspieszeniem kątowym. \(M\) jest momentem siły wypadkowej względem punktu zawieszenia \(M=-mgl\sin\alpha\).
Równanie różniczkowe drgań harmonicznych:
Równanie różniczkowe ruchu wahadła otrzymujemy z II zasady dynamiki ruchu obrotowego \(I\varepsilon=M\), gdzie \(I=ml^2\) jest momentem bezwładności punktu materialnego o masie \(m\) względem osi obrotu, a \(\displaystyle{\varepsilon=\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}}\) jest przyspieszeniem kątowym. \(M\) jest momentem siły wypadkowej względem punktu zawieszenia \(M=-mgl\sin\alpha\).
Równanie różniczkowe drgań harmonicznych:
\(\displaystyle{\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}+\frac{g}{l}\alpha=0 }\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- odległość od środka poziomej platformy karuzeli \(R\),
- długość wahadła \(l\),
- prędkość kątowa karuzeli \(\omega\).
Szukane:
- okres drgań wahadła matematycznego \(T\).
Analiza sytuacji
Równanie różniczkowe ruchu wahadła otrzymujemy z II zasady dynamiki ruchu obrotowego
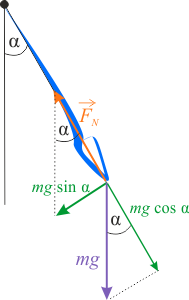
\(I\varepsilon=M\)
\(\displaystyle{ml^2}\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}=-mg\sin\alpha\)
\(\displaystyle{ml^2}\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}=-mg\sin\alpha\)
Dla małych kątów \(M\approx-mgl\alpha\) i stąd mamy:
\(\displaystyle{\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}+\frac{g}{l}\alpha=0 }\)
Przyrównując to równanie z ogólnym równaniem drgań opisywanych zmienną kątową:
\(\displaystyle{\frac{\mathrm{d}^2\alpha }{\mathrm{d} t^2}+\omega^2\alpha=0 }\)
mamy \(\displaystyle{\omega=\sqrt{\frac{g}{l}} }\)
Równanie, które pozwala obliczyć okres drgań wahadła ma postać
\(\displaystyle{T=\frac{2\pi}{\omega}=2\pi \sqrt{\frac{l}{g}} }\)
W omawianym przykładzie (wahadło znajduje się na karuzeli, która obraca się ze stałą prędkością) na wahadło działa również siła dośrodkowa. W takim przypadku mamy
\(\displaystyle{T=2\pi \sqrt{\frac{lm}{F_N}} }\)
Siłę naciągu nici możemy wyznaczyć z zależności: \(F_N=\sqrt{(mg)^2+(ma_d)^2}\) - siła naciągu jest wypadkową siły ciężkości i siły dośrodkowej \(F_d=ma_d\).
\(F_N=m\sqrt{g^2+a_d^2}=m\sqrt{g^2+(\omega^2R)^2}\)
Okres drgań wynosi więc
\(\displaystyle{T=2\pi \sqrt{\frac{lm}{m\sqrt{g^2+(\omega^2R)^2}}} }\)
\(\displaystyle{T=2\pi \sqrt{\frac{l}{\sqrt{g^2+(\omega^2R)^2}}} }\)
Odpowiedź
Okres drgań wahadła matematycznego wiszącego na obracającej się karuzeli wynosi \(\displaystyle{T=2\pi \sqrt{\frac{l}{\sqrt{g^2+(\omega^2R)^2}}} }\).
