Zadanie 6.5.2.1
Fala sinusoidalna w strunie
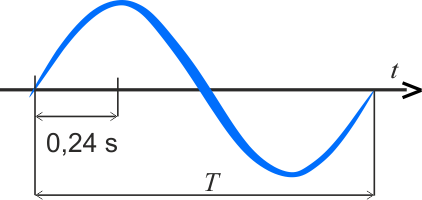
Fala sinusoidalna o długości \(1,56\,\mathrm{m}\) biegnie w napiętej strunie. Punkty struny przebywają drogę od swego położenia równowagi do maksymalnego wychylenia (odkształcenia) w czasie \(0,24\,\mathrm{s}\). Oblicz okres, częstotliwość i prędkość tej fali.
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- długość sinusoidalnej fali \(\lambda=1,56\,\mathrm{m}\),
- czas przebycia drogi przez punkty struny od swego położenia równowagi do maksymalnego wychylenia \(t=0,24\,\mathrm{s}\).
Szukane:
- okres \(T\),
- częstotliwość \(f\),
- prędkość fali \(c\).
Odpowiedź
Szukane wielkości wynoszą:
- okres \(T=0,96\,\mathrm{s}\),
- częstotliwość \(f=1,04\,\mathrm{Hz}\),
- prędkość fali \(\displaystyle{c=1,625\,\mathrm{\frac{m}{s}}}\).
Polecenie
Wyznacz okres fali. Wybierz jedną prawidłową wartość, wśród czterech przedstawionych poniżej.
Wybór 1 z 4
\(T=0,24\,\mathrm{s}\)
\(T=0,24\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Wybór 2 z 4
\(T=0,48\,\mathrm{s}\)
\(T=0,48\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Wybór 3 z 4
\(T=0,72\,\mathrm{s}\)
Odpowiedź nieprawidłowa
Wybór 4 z 4
\(T=0,96\,\mathrm{s}\)
Odpowiedź prawidłowa
Polecenie
Wyznacz częstotliwość oraz prędkość tej fali. Wybierz jeden prawidłowy zestaw wartości, wśród dwóch przedstawionych poniżej.
Wybór 1 z 2
\(f=1,04\,\mathrm{Hz}\)
\(\displaystyle{c=1,498\,\mathrm{\frac{m}{s}}}\)
\(f=1,04\,\mathrm{Hz}\)
\(\displaystyle{c=1,498\,\mathrm{\frac{m}{s}}}\)
Odpowiedź nieprawidłowa
Wybór 2 z 2
\(f=1,04\,\mathrm{Hz}\)
\(\displaystyle{c=1,625\,\mathrm{\frac{m}{s}}}\)
Odpowiedź prawidłowa
Rozwiązanie
Częstotliwość fali wynosi
\(\displaystyle{f=\frac{1}{T}=\frac{1}{0,96}}\)
\(f=1,04\,\mathrm{Hz}\)
Prędkość tej fali wyznaczamy ze wzoru
\(\displaystyle{c=\frac{\lambda}{T}=\frac{1,56}{0,96} }\)
\(\displaystyle{c=1,625\,\mathrm{\frac{m}{s}}}\)
Odpowiedź
Szukane wielkości wynoszą:
- okres \(T=0,96\,\mathrm{s}\),
- częstotliwość \(f=1,04\,\mathrm{Hz}\),
- prędkość fali \(\displaystyle{c=1,625\,\mathrm{\frac{m}{s}}}\).