Zadanie 7.1.1.1
- Materiał 1: średnica wynosi \(1\,\mathrm{mm}\), długość \(80\,\mathrm{m}\), opór właściwy \(1,75\cdot 10^{-8}\,\mathrm{\Omega \cdot m}\)
- Materiał 2: średnica wynosi \(1\,\mathrm{mm}\), długość \(80\,\mathrm{m}\), przewodność elektryczna właściwa \(35,3\cdot 10^{6}\,\mathrm{\frac{S}{m}}\)
Wskazówka teoretyczna
Współczynnik proporcjonalności \(\rho\) nazywa się elektrycznym oporem właściwym materiału (zwany też rezystywnością), z którego wykonany jest przewodnik. Jednostką rezystywności jest \(\,\mathrm{\Omega \cdot m}\).
Przewodność właściwa materiału \(\sigma\) (zwana też konduktywnością) jest wielkością określającą własności przewodzące przewodnika. Konduktywność jest odwrotnością rezystywności. Jednostką przewodności właściwej jest simens przez metr: \(\displaystyle{\,\mathrm{\frac{S}{m} }}\).
Przewodnik o określonym oporze \(R\) nazywa się opornikiem.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane (punkt a):
- stosunek średnic \(d_1=2 d_2\),
- rezystancja dwóch oporników jest taka sama \(R_1=R_2\),
- ten sam materiał \(\rho_1=\rho_2=\rho\).
Dane (punkt b):
- średnica obu drutów \(d_1=d_2=d=1\cdot 10^{-3}\,\mathrm{m}\),
- długość obu drutów \(L_1=L_2=L=80\,\mathrm{m}\),
- opór właściwy \(\rho=1,75\cdot 10^{-8}\,\mathrm{\Omega \cdot m}\),
- przewodność elektryczna właściwa \(\sigma = 35,3\cdot 10^{6}\,\mathrm{\frac{S}{m}}\).
Szukane:
- Punkt a): stosunek długości dwóch kawałków drutu \(\displaystyle{\frac{L_1}{L_2}}\).
- Punkt b): opór rezystorów \(R_1\) oraz \(R_2\).
Analiza sytuacji
Opór jednorodnego przewodnika cylindrycznego możemy wyznaczyć z zależności \(\displaystyle{R=\rho\frac{L}{S} }\),
przy czym przekrój poprzeczny ma kształt koła, więc jego pole powierzchni wynosi \(\displaystyle{S=\pi r^2=\pi \left ( \frac{d}{2} \right )^2}\).
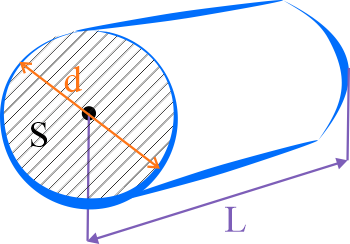
Po podstawieniu mamy: \[\displaystyle{R=\frac{4\rho L}{\pi d^2} }\]
Jeżeli mamy podaną przewodność właściwą materiału \(\sigma\), a nie opór właściwy \(\rho\), rezystancję obliczamy następująco \[\displaystyle{R=\frac{4L}{\sigma\pi d^2} }\]
Rozwiązanie
Punkt a)
Dla warunku takich samych rezystancji dwóch oporników możemy zapisać
\(\displaystyle{\rho\frac{4L_1}{\pi d_1^2}= \rho\frac{4L_2}{\pi d_2^2}}\)
Po przekształceniach \[\displaystyle{\frac{L_1}{d_1^2}=\frac{L_2}{d_2^2}}\] \[\displaystyle{\frac{L_1}{4d_2^2}=\frac{L_2}{d_2^2}}\] \[\displaystyle{\frac{L_1}{L_2}= \frac{4d_2^2}{d_2^2}}\] \[\displaystyle{\frac{L_1}{L_2}=4}\] otrzymujemy
Widać więc, że drut drugi o dwa razy mniejszej średnicy, musi być cztery razy dłuższy od drutu pierwszego o większej średnicy, aby rezystancja tych dwóch elementów była taka sama.
Punkt b)
Opór rezystora \(R_1\) obliczamy z zależności
\[\displaystyle{R_1=\frac{4\rho L}{\pi d^2} }\]
\[\displaystyle{R_1=\frac{4\cdot 1,75\cdot 10^{-8}\cdot 80}{3,14\cdot 0,001^2}\approx 1,7825\,\mathrm{\Omega} }\]
Jednostki:
\[\displaystyle{\mathrm{\frac{\Omega \cdot m \cdot m}{m^2}=\Omega} }\]
Dla rezystora \(R_2\) obliczenia przeprowadzamy według zależności \[\displaystyle{R_2=\frac{4L}{\sigma\pi d^2} }\]
\[\displaystyle{R_2=\frac{4\cdot 80}{35,3\cdot 10^6\cdot 3,14\cdot 0,001^2}\approx 2,8855\,\mathrm{\Omega} }\]
Jednostki:
\[\displaystyle{ \,\mathrm{\frac{m}{m^2\cdot\frac{S}{m}}=\frac{1}{S}=\Omega }}\]
zawiera przykładowe wartości rezystywności i konduktywności dla sześciu wybranych przewodników w temperaturze \(20^{\circ}\,\mathrm{C}\). W tabeli możesz sprawdzić z jakich materiałów wykonano druty.
| Nazwa materiału | Rezystywność \(\rho\)\(\left [\,\mathrm{\Omega\cdot m}\right ]\) | Konduktywność \(\sigma\)\(\displaystyle{\left [\mathrm{\frac{S}{m}}\right ]}\) | ||||||||||||||||||
|
|
|
Odpowiedź
Stosunek długości dwóch kawałków drutu, wykonanych z takich samych materiałów, ale o dwukrotnej różnicy w średnicach, wynosi \(\displaystyle{\frac{L_1}{L_2}=4 }\).
Dla punktu b) wartości rezystancji są następujące: \[\displaystyle{R_1=1,8\,\mathrm{\Omega} }\] \[\displaystyle{R_2=2,9\,\mathrm{\Omega} }\]
