Zadanie 7.1.1.2
Wskazówka teoretyczna
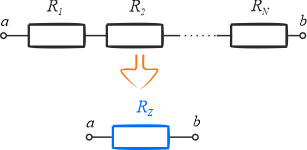
Opór zastępczy wyznaczamy następująco: \[R_Z=R_1+R_2+...+R_N\]
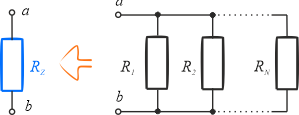
Połączeniem równoległym oporników nazywa się takie połączenie, przy którym początki wszystkich oporników łączą się w jednym węźle, a końce w drugim.
Opór zastępczy wyznaczamy następująco: \[\displaystyle{\frac{1}{R_Z}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_N} } \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wartości rezystancji: \(R_1=R_2=R_4=R_8=100\,\mathrm{\Omega}\), \(R_5=R_9=200\,\mathrm{\Omega}\), \(R_3=R_6=400\,\mathrm{\Omega}\) oraz \(R_7=300\,\mathrm{\Omega}\).
Szukane:
- rezystancja zastępcza układu \(R_Z\).
Analiza sytuacji
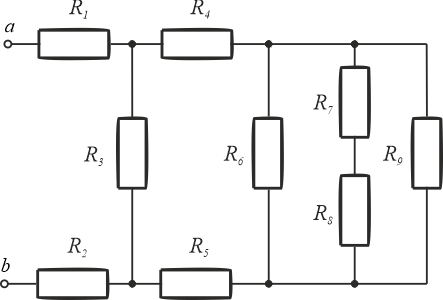
Przedstawiony schemat dziewięciu rezystorów jest na tyle skomplikowany, że najwygodniej wyznaczyć rezystancję zastępczą w kilku krokach. Zaciski \(ab\) są z lewej strony układu rezystorów, więc upraszczanie układu zaczniemy z drugiej strony.
Rozwiązanie
Krok 1
Zauważmy, że rezystory \(R_7\) oraz \(R_8\) połączone są szeregowo (pomiędzy nimi nie ma węzła). Zamiast tych dwóch oporników można narysować jeden o rezystancji:
\[R_{78}=R_7+R_8=300\,\mathrm{\Omega}+100\,\mathrm{\Omega}=400\,\mathrm{\Omega}\]
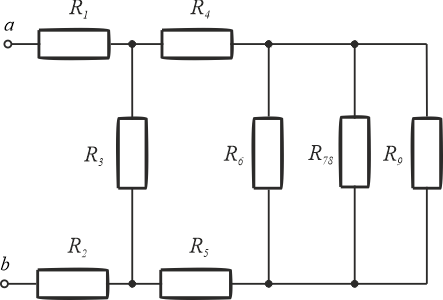
Krok 2
Trzy rezystory \(R_6\), \(R_{78}\) oraz \(R_9\) połączone są równolegle. Oporniki te możemy zastąpić jednym o rezystancji \(R_{6-9}\).
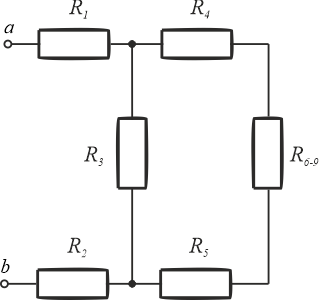
Rezystancję \(R_{6-9}\) można policzyć następująco:
\[\displaystyle{\frac{1}{R_{6-9}}=\frac{1}{R_6}+\frac{1}{R_{78}}+\frac{1}{R_9} } \]
\[\displaystyle{\frac{1}{R_{6-9}}=\frac{1}{400}+\frac{1}{400}+\frac{1}{200}=\frac{1}{100} } \]
Rezystancja \(R_{6-9}\) wynosi więc \(100\,\mathrm{\Omega}\). Pokazane wyżej obliczenia można przeprowadzić na symbolach \[\displaystyle{\frac{1}{R_{6-9}}=\frac{1}{R_6}+\frac{1}{R_{78}}+\frac{1}{R_9}}\] \[\displaystyle{\frac{1}{R_{6-9}}=\frac{R_6+R_{78}}{R_6\cdot R_{78}}+\frac{1}{R_9}}\] \[\displaystyle{\frac{1}{R_{6-9}}=\frac{\left (R_6+R_{78}\right )R_9+R_6R_{78}}{R_6R_{78}R_9}}\] i uzyskać wzór, do którego podstawiamy dane:
\[\displaystyle{R_{6-9}=\frac{R_6R_{78}R_9}{R_6R_9+R_{78}R_9+R_6R_{78}}}\]
\[\displaystyle{R_{6-9}=\frac{400\cdot 400\cdot 200}{400\cdot 200+400\cdot 200+400\cdot 400}=100\,\mathrm{\Omega} }\]
INFORMACJA DODATKOWA
W przypadku, gdy wartości połączonych oporników są takie same, powyższy wzór można uprościć do postaci:
\[\displaystyle{R_Z=\frac{R\cdot R\cdot R}{R\cdot R+R\cdot R+R\cdot R}=\frac{R^3}{3R^2} }\]
\[\displaystyle{R_Z=\frac{R}{3} }\]
Dla \(\mathrm{N}\) takich samych oporników połączonych równolegle można więc napisać
\[\displaystyle{R_Z=\frac{R}{\mathrm{N}} }\]
Następne kroki
Krok 3
Rezystory \(R_4\), \(R_5\) oraz \(R_{6-9}\) połączone są szeregowo. Policzmy teraz rezystancję opornika \(R_{4-9}\), który zastąpi te trzy rezystory.
\[R_{4-9}=R_4+R_5+R_{6-9}=100\,\mathrm{\Omega}+200\,\mathrm{\Omega}+100\,\mathrm{\Omega}\]
\[R_{4-9}=400\,\mathrm{\Omega}\]
Po uproszczeniu układu otrzymujemy następujący schemat połączeń.
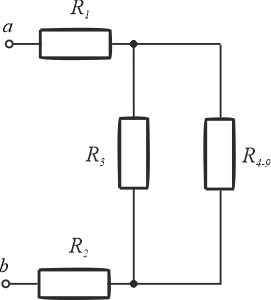
Krok 4
Rezystory \(R_3\) oraz \(R_{4-9}\) połączone są równolegle i mają taką samą wartość, możemy więc zapisać:
\[R_{3-9}=\frac{R_3}{2}=\frac{400}{2}=200\,\mathrm{\Omega}\]
Po tej operacji otrzymujemy ponownie trzy oporniki połączone szeregowo \(R_1\), \(R_2\) oraz \(R_{3-9}\)
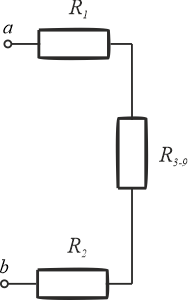
Krok 5
Rezystancja zastępcza wynosi:
\[R_Z=R_1+R_2+R_{3-9}=100\,\mathrm{\Omega}+100\,\mathrm{\Omega}+200\,\mathrm{\Omega}\]
\[R_Z=400\,\mathrm{\Omega}\]
Odpowiedź
Rezystancja zastępcza wynosi: \(R_Z=400\,\mathrm{\Omega}\).
