Zadanie 7.1.1.3
Wskazówka teoretyczna
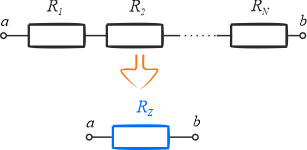
Opór zastępczy wyznaczamy następująco: \[R_Z=R_1+R_2+...+R_N\]
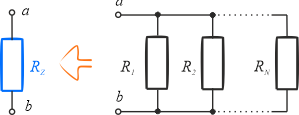
Połączeniem równoległym oporników nazywa się takie połączenie, przy którym początki wszystkich oporników łączą się w jednym węźle, a końce w drugim.
Opór zastępczy wyznaczamy następująco: \[\displaystyle{\frac{1}{R_Z}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_N} } \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wartości rezystancji: \(R\)
Szukane:
- rezystancja zastępcza układu od strony zacisków \(ab\): \(R_{ab}\),
- rezystancja zastępcza układu od strony zacisków \(cd\): \(R_{cd}\).
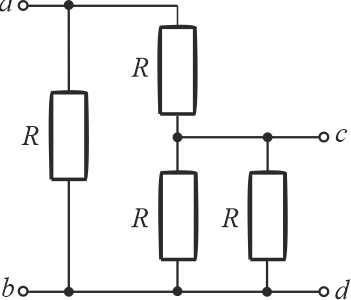
Zaciski \(ab\)
Wyznaczając rezystancję zastępczą układu rezystorów ze strony zacisków \(ab\), traktujemy schemat tak jakby nie było zacisków \(cd\). Obliczenia zaczynamy od prawej strony schematu.
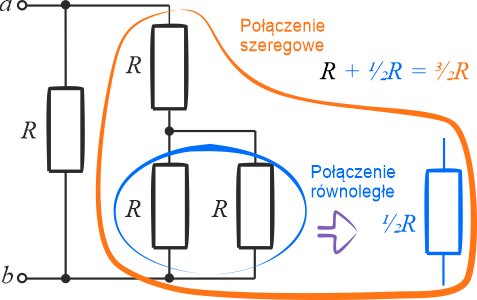
Dwa rezystory z prawej strony są połączone równolegle (niebieska obwiednia na powyższym rysunku). Jeżeli rezystory te mają taką samą wartość, to możemy napisać:
\[\displaystyle{R_1=\frac{R}{2} }\]
Następnie rezystor \(R_1\) tworzy szeregowe połączenie z rezystorem \(R\) znajdującym się nad nim. Tak więc mamy \(\displaystyle{R_2=R+\frac{R}{2}=\frac{3R}{2} }\). W ten sposób otrzymujemy dwa rezystory połączone równolegle.
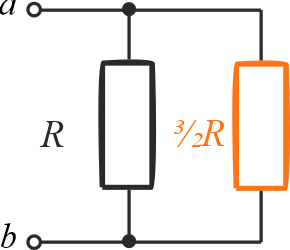
Rezystancja zastępcza wynosi
\[\displaystyle{R_{ab}=\frac{\frac{3}{2}R\cdot R}{\frac{3}{2}R+R}=\frac{3}{2}R\cdot \frac{2}{5} }\]
\[\displaystyle{R_{ab}=\frac{3}{5}\,R }\]
Zaciski \(cd\)
Ze strony zacisków \(cd\) schemat wygląda następująco:
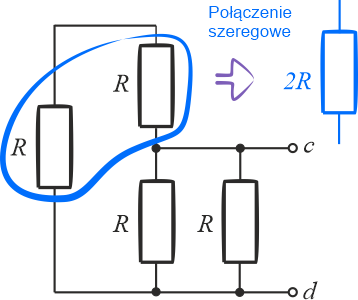
Tym razem zaczynamy obliczenia z lewej strony układu (przeciwna strona do zacisków - na rysunku powyżej zaznaczona niebieską obwiednią). Dwa rezystory połączone są szeregowo. Po zsumowaniu wartości oporników \(R+R\) otrzymujemy układ trzech rezystorów połączonych równolegle.
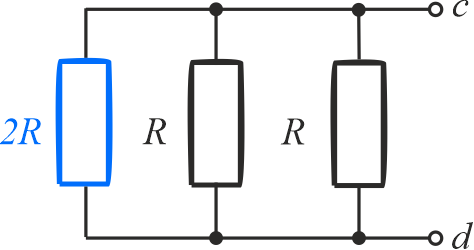
Rezystancja zastępcza wynosi
\[\displaystyle{\frac{1}{R_{cd}}=\frac{1}{2R}+\frac{1}{R}+\frac{1}{R}=\frac{5}{2R} }\]
\[\displaystyle{R_{cd}=\frac{2}{5}R }\]
Kolejny etap
Rezystancja zastępcza ze strony różnych zacisków może być taka sama lub różna. Zależy to oczywiście od konfiguracji układu i wartości rezystorów. W omawianym przypadku (wartości rezystorów są takie same), obie te rezystancje zastępcze są różne. Te same wartości rezystancji zastępczej możemy otrzymać tylko w przypadku, gdy wartości oporników będą nie takie same. Dla ułatwienia oznaczmy wszystkie rezystory.
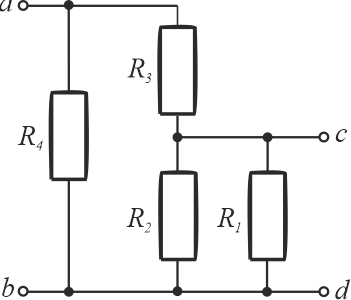
Te same rezystancje zastępcze otrzymamy, gdy. np. \(R_1=R_2\), rezystor \(R_4\) będzie miał wartość o połowę mniejszą od \(R_1\), czyli \(\displaystyle{R_4=\frac{1}{2}R_1 }\), a opornik \(R_3\) może mieć dowolną wartość. Przykładowo: \(R_1=R_2=1\,\mathrm{k\Omega}\) oraz \(R_4=0,5\,\mathrm{k\Omega}\).
Do obliczenia rezystancji zastępczych, w tym przypadku, można użyć poniższych wzorów lub postępować etapami, jak to było pokazywane wyżej.
\[\displaystyle{R_{ab}=\frac{R_4\left ( R_1R_2+R_1R_3+R_2R_3 \right )}{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_2R_4} }\]
\[\displaystyle{R_{cd}=\frac{R_1R_2R_3+R_1R_2R_4}{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_2R_4} }\]
Odpowiedź
Rezystancja zastępcza układu od strony zacisków \(ab\) wynosi \(\displaystyle{R_{ab}=\frac{3}{5}R }\), natomiast rezystancja zastępcza układu od strony zacisków \(cd\) \(\displaystyle{R_{cd}=\frac{2}{5}R }\). Możliwe jest aby rezystancje zastępcze od strony zacisków \(ab\) oraz \(cd\) były takie same.
