Zadanie 7.1.1.4
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 7. Elektryczność
  3. 7.1. Zagadnienia związane z rezystancją
  4. 7.1.1. Nauka
  5. Zadanie 7.1.1.4

 Zadanie 7.1.1.4

Współczynnik cieplny
Oblicz wartość współczynnika cieplnego oporu przewodnika składającego się z drutu aluminiowego o oporze \(3\,\mathrm{\Omega}\) (dla temperatury \(0^o\,\mathrm{C}\)) oraz z drutu z żelaza o oporze \(2\,\mathrm{\Omega}\) (dla temperatury \(0^o\,\mathrm{C}\)), połączonych szeregowo. Współczynniki cieplne użytych materiałów wynoszą: \(\displaystyle{\alpha_A=3,9\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\) oraz \(\displaystyle{\alpha_{Fe}=5\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\).

 Wskazówka teoretyczna

 Teoria - zależność oporu od temperatury
Przy niezbyt dużej różnicy temperatur zależność oporu elektrycznego przewodnika od temperatury z, dostateczną dokładnością, wyraża wzór
\[R_T=R_0\left [ 1+\alpha\left ( T-T_0 \right ) \right ]\]
gdzie: \(R_T\) - opór w temperaturze \(T\), \(R_0\) - opór w temperaturze \(T_0\), \(\alpha\) - współczynnik cieplny oporu.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- drut aluminiowy

opór \(R_{0A}=3\,\mathrm{\Omega}\) (dla temperatury \(0^o\,\mathrm{C}\))
współczynnik cieplny \(\displaystyle{\alpha_A=3,9\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\)
- drut z żelaza
opór \(R_{0Fe}=2\,\mathrm{\Omega}\) (dla temperatury \(0^o\,\mathrm{C}\))
współczynnik cieplny \(\displaystyle{\alpha_{Fe}=5\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\)

Szukane:
- wartość współczynnika cieplnego oporu przewodnika składającego się z dwóch różnych drutów \(\alpha\).

Analiza sytuacji

W temperaturze \(0^o\,\mathrm{C}\) rezystancja wypadkowa dwóch szeregowo połączonych rezystorów, wykonanych z różnych materiałów wynosi
\[R_0=R_{0A}+R_{0Fe}\]
Po podniesieniu temperatury (w niedużym zakresie) opór wypadkowy zmieni się i wyniesie
\[R=R_A+R_{Fe}\]
Rezystancje \(R_A\) oraz \(R_{Fe}\) są oporami drutu z aluminiom i z żelaza po podniesieniu temperatury. Opory te będą większe od rezystancji w temperaturze zera stopni Celsjusza.

Rozwiązanie

Rezystancja elementu wykonanego z dwóch rożnych materiałów, w temperaturze wyższej od zera stopni Celsjusza, wynosi
\[R_0\left (1+\alpha \Delta T\right )=R_{0A}\left (1+\alpha_A \Delta T\right )+R_{0Fe}\left (1+\alpha_{Fe} \Delta T\right )\]
\[R_0+R_0\alpha \Delta T=R_{0A}+R_{0A}\alpha_A \Delta T+R_{0Fe}+R_{0Fe}\alpha_{Fe} \Delta T\]
Ponieważ \(R_0=R_{0A}+R_{0Fe}\), możemy zapisać
\[R_0+R_0\alpha \cancel{\Delta T}=R_0+R_{0A}\alpha_A \cancel{\Delta T}+R_{0Fe}\alpha_{Fe} \cancel{\Delta T}\]
\[R_0\alpha =R_{0A}\alpha_A+R_{0Fe}\alpha_{Fe}\]
\[\displaystyle{\alpha=\frac{R_{0A}\alpha_A+R_{0Fe}\alpha_{Fe}}{R_{0A}+R_{0Fe}} }\]
\[\displaystyle{\alpha=\frac{3\cdot 3,9\cdot 10^{-3}+2\cdot 5\cdot 10^{-3}}{3+2} }\]
\[\displaystyle{\alpha=4,34\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\]

Zależność oporu właściwego \(\rho\) od temperatury jest liniowa:
\[\rho=\rho_0\left (1+\alpha\Delta T\right )\]
Ma to miejsce w temperaturach bliskich temperatury pokojowej oraz wyższych. W niskich temperaturach zależność przestaje być liniowa.



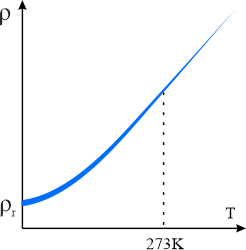
W temperaturze \(0\,\mathrm{K}\) występuje, tzw. opór resztkowy \(\rho_r\), którego wartość zależy od czystości materiału i obecności resztkowych naprężeń.

Przewodnictwo elektryczne właściwe \(\sigma\) jest odwrotnością oporu elektrycznego właściwego \(\rho\). Zależność \(\sigma(T)\) przedstawiona jest poniżej.

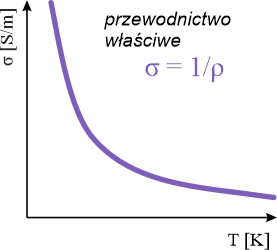
Odpowiedź

Wartość współczynnika cieplnego oporu przewodnika składającego się z dwóch różnych drutów wynosi \(\displaystyle{\alpha=4,34\cdot 10^{-3} \,\mathrm{\frac{1}{K}}}\).