Analiza sytuacji

Napięcie mierzymy woltomierzem, który należy podłączyć równolegle. W tym przypadku mierzymy spadek napięcia na rezystorze, więc miernik podłączamy tak jak na poniższym rysunku.

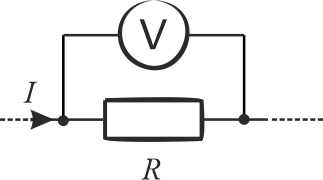
Wartość natężenia prądu wyznaczamy z prawa Ohma
\[\displaystyle{I=\frac{U}{R}=\frac{1,965}{1000}=0,001965\,\mathrm{A} }\]
\[I=1,965\,\mathrm{mA}\]

Niepewności pomiarowe

W danym przypadku wartość zmierzoną otrzymujemy poprzez obliczenia na bazie prawa Ohma. Niepewności pomiarowe w takiej sytuacji są złożone. W celu obliczenia niepewności złożonej natężenia prądu, musimy najpierw przeliczyć niepewności graniczne - podawane przez producentów - na niepewności standardowe.

Niepewności standardowe

Rezystor
Klasa rezystora mówi nam o niepewności granicznej względnej (wyrażonej w procentach). Możemy więc zapisać niepewność względną graniczną

\(\delta R=1\%\)
Niepewność bezwzględna wynosi
\(\Delta R = 1000\,\mathrm{\Omega}\cdot 1\%=10\,\mathrm{\Omega}\)
Niepewności graniczne przeliczamy na niepewności standardowe według zależności
\(\displaystyle{u\left ( R \right )=\frac{\Delta R}{\sqrt{3}} }\)
\(\displaystyle{u\left ( R \right )=\frac{10}{\sqrt{3}}=5,773\,\mathrm{\Omega} }\)
Niepewność standardowa względna wynosi
\(\displaystyle{u_r\left ( R \right )=\frac{5,773}{1000}\cdot 100\%=0,58\% }\)
Pomiar napięcia
Formuła do policzenia niepewności granicznej pomiaru napięcia ma postać \(\left ( \pm 0,5\%+2\right )\). Zapis ten jest skrócony. Część pierwsza tej formuły mówi przez ile procent należy pomnożyć wartość zmierzoną, a druga związana jest z rozdzielczością pomiaru. W tym przypadku rozdzielczość wynosi \(0,001\,\mathrm{V}\), co widać choćby po odczycie wielkości mierzonej (jest również podawana w dokumentacji przyrządu). \(2\) oznacza, że należy rozdzielczość pomnożyć przez \(2\):
\(\Delta U=1,965\cdot 0,5\%+0,001\cdot 2\)
\(\Delta U=1,965\cdot 0,005+0,002=0,01183\,\mathrm{V}\)
Mamy niepewność graniczną bezwzględną i możemy przeliczyć ją na odchylenie standardowe.
\(\displaystyle{u\left ( U \right )=\frac{\Delta U}{\sqrt{3}} }\)
\(\displaystyle{u\left ( U \right )=\frac{0,01183}{\sqrt{3}}=0,006827\,\mathrm{V} }\)
Niepewność standardowa względna wynosi
\(\displaystyle{u_r\left ( U \right )=\frac{0,006827}{1,965}\cdot 100\%=0,35\% }\)

Niepewność złożona
Niepewność złożoną wyliczamy korzystając z wyznaczonych niepewności standardowych pomiarów pośrednich, w tym przypadku z \(u\left ( R \right )\) oraz \(u\left ( U \right )\). Ogólnie można ją policzyć z zależności
\(\displaystyle{u\left ( y \right )=\sqrt{\Sigma_i^k \left (\frac{\partial f}{\partial x_i}\right )^2u^2\left ( x_i \right )}}\)
 Szczegółowe obliczenia pokażą się poniżej. Ponieważ w prawie Ohma występuje tylko mnożenie (lub dzielenie) możemy obliczenia uprości, korzystając z prawa propagacji niepewności.
\(u_r\left ( I \right )=\sqrt{u_r^2\left ( R \right )+u_r^2\left ( U \right )}\)
\(u_r\left ( I \right )=\sqrt{\left ( 0,58 \right )^2+\left ( 0,35 \right )^2}=0,68\%\)
Dalej otrzymujemy:
\(u\left ( I \right )=1,965\,\mathrm{mA}\cdot 0,68\%=0,01336\,\mathrm{mA}\)

Niepewność rozszerzona dla \(k=2\), czyli przedziału ufności \(95%\), wynosi \(U\left ( I \right )=0,01336\cdot 2=0,027\,\mathrm{mA}\)

Ostatecznie otrzymujemy natężenie zmierzonego prądu \(I=\left (1,965\pm 0,027\right )\,\mathrm{mA}\)