Zadanie 7.1.2.5
a) prąd ma stałe natężenie \(0,4\,\mathrm{A}\)
b) prąd wzrasta jednostajnie od zera do \(0,3\,\mathrm{A}\).
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- czas przepływu prądu \(t=20\,\mathrm{s}\),
- stałe natężenie prądu \(I_1=0,4\,\mathrm{A}\),
- wartość zmieniającego się prądu po czasie \(t\): \(I_2=0,3\,\mathrm{A}\).
Szukane:
- ładunek elektryczny płynący przez przewodnik przy stałym prądzie \(Q_1\),
- ładunek elektryczny płynący przez przewodnik przy wzrastającym prądzie \(Q_2\).
Odpowiedź
Wartości ładunków wynoszą odpowiednio \(Q_1=8\,\mathrm{C}\) oraz \(Q_2=3\,\mathrm{C}\).
Polecenie
Jaki ładunek elektryczny przepłynie przez przewodnik, gdy prąd ma stałe natężenie \(I_1=0,4\,\mathrm{A}\)? Wybierz jedną prawidłową wartość spośród czterech.
\(Q_1=2\,\mathrm{C}\)
\(Q_1=3\,\mathrm{C}\)
Rozwiązanie
Natężenie prądu \(I\) mówi o zmianie ładunku \(\,\mathrm{d}Q\) przepływającego przez poprzeczny przekrój przewodnika w czasie \(\,\mathrm{d}t\):
\[\displaystyle{I=\frac{\mathrm{d} Q}{\mathrm{d} t}}\]
W przypadku stałego prądu możemy zapisać \(\displaystyle{I_1=\frac{Q_1}{t} }\), a po przekształceniu mamy
\[Q_1=I_1\cdot t=0,4\,\mathrm{A}\cdot 20\,\mathrm{s}=8\,\mathrm{C}\]
Polecenie
Jaki ładunek elektryczny przepłynie przez przewodnik, gdy natężenie prądu wzrasta do wartości \(I_2=0,3\,\mathrm{A}\) w czasie \(t=20\,\mathrm{s}\)? Wybierz jedną prawidłową wartość spośród czterech.
Rozwiązanie
W przypadku zmiany prądu możemy zapisać \(\displaystyle{I_2=\frac{\mathrm{d} Q_2}{\mathrm{d} t}}\), a po przekształceniu mamy
\[\displaystyle{\mathrm{d} Q_2=I_2\cdot {\mathrm{d} t}}\]
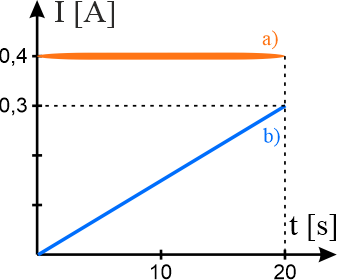
Parametry równania funkcji określającej wzrost prądu odczytujemy z wykresu. Na wykresy wzrost prądu zaznaczony jest niebieską linią - jest to funkcja liniowa o początku w punkcie \((0,0)\). Równanie prostej ma postać \(I(t)=a\cdot t\), gdzie \(a\) jest współczynnikiem nachylenia o jednostce \(\displaystyle{\mathrm{\frac{A}{s}}}\). Współczynnik \(a\) wynosi:
\[0,3=a\cdot 20\]
\[\displaystyle{a=\frac{3}{200}\,\mathrm{\frac{A}{s}} }\]
Możemy zatem napisać
\[\displaystyle{\mathrm{d} Q_2=\frac{3}{200}\cdot t\cdot {\mathrm{d} t}}\]
Całkując obustronnie mamy
\[\displaystyle{Q_2=\int_{0}^{20}at\mathrm{d}t=\frac{3}{200}\cdot \frac{1}{2}\left [ t^2 \right ]_0^{20}=3\,\mathrm{C}}\]
W przypadku funkcji liniowej nie jest konieczne liczenie całki. Można policzyć pole pod wykresem, a w tym przypadku pole trójkąta prostokątnego o przyprostokątnych długości \(0,3\) oraz \(20\).
Polecenie
Wskaż symbol elementu, który umożliwia stały liniowy wzrost prądu. Wybierz jeden prawidłowy symbol spośród dwóch.
Jest to symbol rezystora.
Jest to symbol rezystora o zmiennej rezystancji, np. rezystora suwakowego.
Odpowiedź
Wartości ładunków wynoszą odpowiednio \(Q_1=8\,\mathrm{C}\) oraz \(Q_2=3\,\mathrm{C}\).