Zadanie 7.2.1.1
Prawa Kirchhoffa
Wyznacz rezystancję zastępczą układu (przedstawionego poniżej) na bazie praw Kirchhoffa oraz przekształcenia "trójkąt-gwiazda" na zaciskach \(ab\).
Wskazówka teoretyczna
Teoria - prawa Kirchhoffa
I prawo Kirchhoffa - twierdzenie o punkcie rozgałęzienia
Algebraiczna suma prądów schodzących się w węźle jest równa zeru, przy czym prądy wpływające do węzła są dodatnie, a wypływające - ujemne.
\[\sum_{k=1}^{n}I_k=0\]
II prawo Kirchhoffa - twierdzenie o obwodzie zamkniętym
Algebraiczna suma sił elektromotorycznych i przyrostów napięć w dowolnym obwodzie zamkniętym jest równa zeru (spadek napięcia jest przyrostem ujemnym napięcia).
\[\sum_{i=1}^{N}\varepsilon_i+\sum_{j=1}^{M} I_jR_j=0\]
Twierdzenie o obwodzie zamkniętym jest wynikiem zasady zachowania energii, a twierdzenie o punkcie rozgałęzienia wynika z zasady zachowania ładunku.
Algebraiczna suma prądów schodzących się w węźle jest równa zeru, przy czym prądy wpływające do węzła są dodatnie, a wypływające - ujemne.
\[\sum_{k=1}^{n}I_k=0\]
II prawo Kirchhoffa - twierdzenie o obwodzie zamkniętym
Algebraiczna suma sił elektromotorycznych i przyrostów napięć w dowolnym obwodzie zamkniętym jest równa zeru (spadek napięcia jest przyrostem ujemnym napięcia).
\[\sum_{i=1}^{N}\varepsilon_i+\sum_{j=1}^{M} I_jR_j=0\]
Twierdzenie o obwodzie zamkniętym jest wynikiem zasady zachowania energii, a twierdzenie o punkcie rozgałęzienia wynika z zasady zachowania ładunku.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
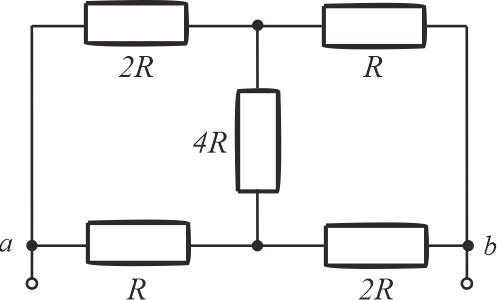
- schemat połączeń oporników.
Szukane:
- rezystancja zastępcza \(R_z\)
Zastosowanie praw Kirchhoffa
Przedstawiony schemat oporników nie jest połączeniem ani szeregowym, ani równoległym. W takim przypadku możemy skorzystać z metody oczkowej. Rozwiązanie zaczniemy od zaznaczenia kierunków prądów i oczek w schemacie.
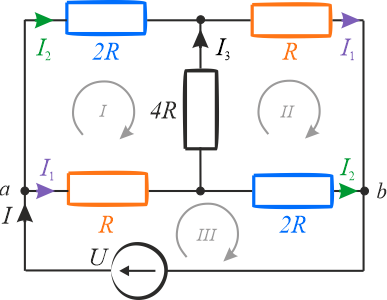
W układzie występują po dwa takie same rezystory, możemy więc zapisać, że przez rezystory \(2R\) płynie prąd \(I_2\), a przez rezystory \(R\) - prąd \(I_1\). Aby w obwodzie płynął prąd, do zacisków \(ab\) należy podłączyć źródło.
I prawo Kirchhoffa
Na schemacie mamy cztery węzły, do których wpływają i wypływają prądy. I prawo Kirchhoffa dla węzła przy punkcie \(a\) oraz \(b\) ma taką samą postać:
\[I=I_1+I_2\]
Do węzła \(a\) wpływa prąd \(I\), a wypływają \(I_1\) oraz \(I_2\), czyli \(I-I_1-I_2=0\), natomiast do węzła \(b\) wpływają \(I_1\) oraz \(I_2\), a wypływa prąd \(I\), co daje: \(-I+I_1+I_2=0\). W wyniku otrzymujemy takie samo równanie.
Do węzła na górze wpływa prąd \(I_2\) oraz \(I_3\), a wypływa prąd \(I_1\): \(I_2+I_3-I_1=0\). Dla ostatniego pozostałego węzła możemy zapisać: \(-I_2-I_3+I_1=0\). W sumie otrzymujemy drugie równanie
\[I_1=I_2+I_3\]
II prawo Kirchhoffa
Oczko to dowolna zamknięta część obwodu złożonego. W przedstawionym schemacie mamy trzy oznaczone oczka. Dla każdego oczka można rozpisać równanie wynikające z drugiego prawa Kirchhoffa.
\[\sum_{j=1}^{M} I_jR_j=\sum_{i=1}^{N}\varepsilon_i\]
Przy stosowaniu tego prawa obowiązuje następująca reguła znaków: prądy i siły elektromotoryczne pokrywające się z dowolnie wybranym kierunkiem obiegu obwodu (np. zgodnie z ruchem wskazówek zegara) przyjmuje się za dodatnie, a skierowane przeciwnie za ujemne.
Zacznijmy od oczka nr I:
Oczko nr II:
Oczko nr III:
Równania dla oczka I oraz oczka II są takie same. Wynika to z budowy układu.
Z praw Kirchhoffa otrzymaliśmy \(4\) równania
\(\left\{\begin{matrix} I=I_1+I_2 &\\ I_1=I_2+I_3 &\\ U=RI_1+2RI_2 &\\ 2RI_2-RI_1-4RI_3=0 \end{matrix}\right. \)
Do równania ostatniego, za prąd \(I_3\) podstawmy \(I_3=I_1-I_2\), otrzymamy: \(2RI_2-RI_1-4RI_1+4RI_2=0\), a po uproszczeniu \(6I_2=5I_1\). Następnie wracamy do równania pierwszego u układu równań:
\[\displaystyle{I=I_1+I_2=\frac{6}{5}I_2+I_2=\frac{11}{5}I_2 }\]
\[\displaystyle{I=I_1+I_2=I_1+\frac{5}{6}I_2=\frac{11}{6}I_1 }\]
Rezystancja zastępcza układu wynosi
\[\displaystyle{R_z=\frac{U}{I}=\frac{RI_1+2RI_2}{I}=\frac{I_1}{I}R+\frac{I_2}{I}2R=\frac{6}{11}R+\frac{10}{11}R=\frac{16}{11}R }\]
Wzory
Przekształcenie trójkąt - gwiazda i gwiazda - trójkąt
Układy połączeń oporników w trójkąt oraz w gwiazdę pokazano poniżej
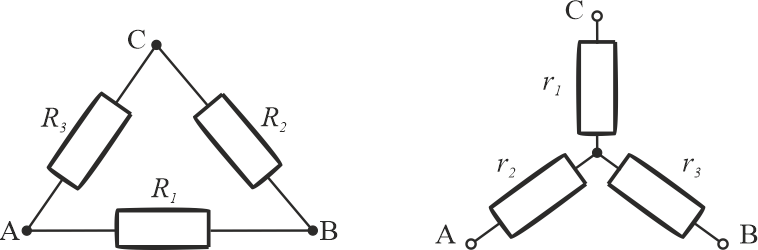
Wzory na przekształcenia trójkąta w gwiazdę i na odwrót otrzymujemy z warunku równości potencjałów:
\[\displaystyle{R_{AB}=\frac{R_1\left (R_2+R_3 \right )}{R_1+R_2+R_3}=r_2+r_3}\]
\[\displaystyle{R_{BC}=\frac{R_2\left (R_1+R_3 \right )}{R_1+R_2+R_3}=r_1+r_3}\]
\[\displaystyle{R_{AC}=\frac{R_3\left (R_1+R_2 \right )}{R_1+R_2+R_3}=r_1+r_2}\]
Odpowiednio przekształcając powyższe trzy równania otrzymujemy
a) przekształcenie trójkąt-gwiazda:
\[\displaystyle{\left\{\begin{matrix} r_1=\frac{R_2R_3}{R_1+R_2+R_3}\\ r_2=\frac{R_1R_3}{R_1+R_2+R_3}\\ r_3=\frac{R_1R_2}{R_1+R_2+R_3} \end{matrix}\right.}\]
b) przekształcenie gwiazda-trójkąt:
\[\displaystyle{\left\{\begin{matrix} R_1=r_2+r_3+\frac{r_2r_3}{r_1}\\ R_2=r_1+r_3+\frac{r_1r_3}{r_2} \\ R_3=r_1+r_2+\frac{r_1r_2}{r_3} \end{matrix}\right.}\]
Przekształcenie trójkąt-gwiazda
Rezystancję zastępczą omawianego układu można wyznaczyć stosując przekształcenie trójkąt-gwiazda. Na rysunku poniżej zaznaczono trzy rezystor, które tworzą połączenie w trójkąt.
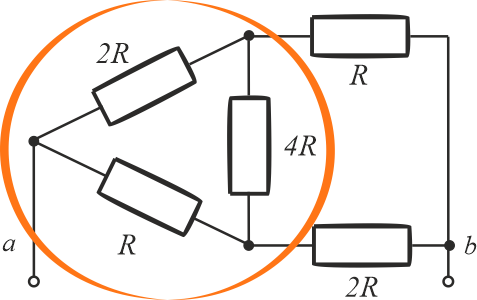
Teraz obliczamy rezystancję trzech rezystorów \(r_1\), \(r_2\) oraz \(r_3\), które utworzą gwiazdę.
\[\displaystyle{\left\{\begin{matrix} r_1=\frac{R\cdot 4R}{R+2R+4R}=\frac{4}{7}R\\ r_2=\frac{2R\cdot 4R}{7R}=\frac{8}{7}R\\ r_3=\frac{2R\cdot R}{7R}=\frac{2}{7}R \end{matrix}\right.}\]
Przekształcony układ wygląda następująco:
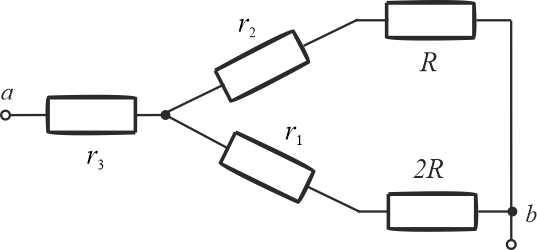
Rezystancja zastępcza wynosi
\[\displaystyle{R_z=r_3+\frac{\left ( r_2+R\right )\left (r_1+2R \right )}{r_1+r_2+R+2R}}\]
\[\displaystyle{R_z=\frac{2}{7}R+\frac{\left ( \frac{8}{7}R+R\right )\left (\frac{4}{7}R+2R \right )}{\frac{4}{7}R+\frac{8}{7}R+3R}=\frac{16}{11}R}\]
Odpowiedź
Rezystancja zastępcza wynosi \(\displaystyle{R_z=\frac{16}{11}R }\).