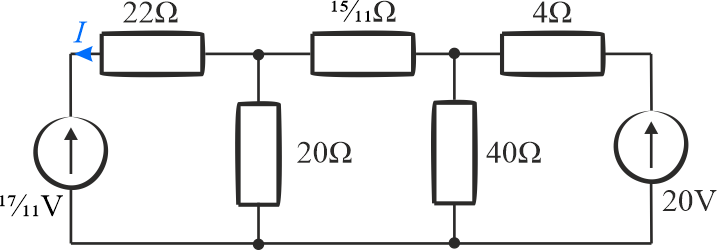
Zadanie 7.2.1.2
Wskazówka teoretyczna
Dowolny źródłowy obwód liniowy można, od strony wybranych zacisków \(AB\), zastąpić obwodem równoważnym złożonym z szeregowo połączonego jednego idealnego źródła napięcia równego napięciu pomiędzy zaciskami \(AB\) w stanie jałowym oraz jednej impedancji równej impedancji zastępczej obwodu bezźródłowego widzianej od strony zacisków \(AB\).
Twierdzenia Nortona
Dowolny aktywny obwód liniowy można od strony wybranych zacisków \(AB\) zastąpić obwodem równoważnym złożonym z równolegle połączonego jednego idealnego źródła prądu o prądzie źródłowym równym prądowi w gałęzi ab przy zwarciu zacisków ab oraz jednej admitancji zastępczej tego obwodu pasywnego widzianej od strony wybranych zacisków \(AB\).
Zastępcze układy Thevenina i Nortona są równoważne między sobą i z układem zastępowanym.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- schemat połączeń oporników i źródeł z wartościami liczbowymi.
Szukane:
- wartość prądu \(I\)
Analiza sytuacji
W układzie mamy dwa źródła napięciowe. Nie możemy zastosować tylko metody uproszczeń rezystancji, ponieważ w ten sposób nie uwzględnimy w przeliczeniach jednego źródła. W tym przypadku zastosujemy metodę transformacji źródeł. Mamy policzyć prąd płynący w gałęzi ze źródłem po lewej stronie schematu, więc obliczenia zaczniemy od strony drugiego źródła napięciowego o napięciu \(20\,\mathrm{V}\).
Na poniższych rysunkach przedstawiono schematy rzeczywistego źródła napięciowego \(a)\) oraz prądowego \(b)\) z odpowiednio podłączoną rezystancją wewnętrzną \(R_w\).
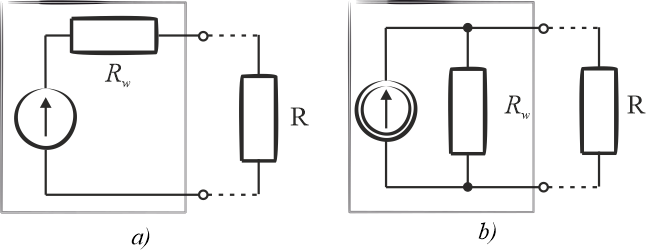
Źródło napięciowe (rysunek \(a\)) - element aktywny, który ma za zadanie utrzymanie na wyjściu określonej wartości napięcia przy różnych poborach prądu.
Źródło prądowe (rysunek \(b\)) - element aktywny, który ma za zadanie utrzymanie na wyjściu określonej wartości prądu przy różnych napiciach.
Rozwiązanie
Etap 1
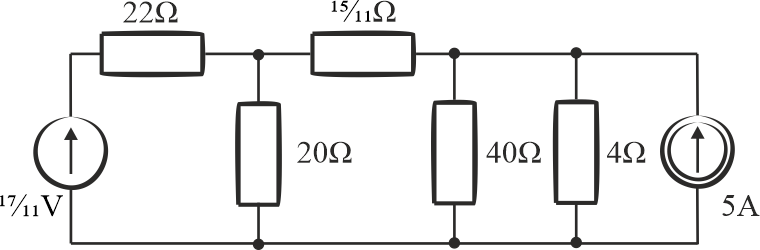
Źródło napięciowe o napięciu \(20\,\mathrm{V}\) i rezystancji wewnętrznej \(4\,\mathrm{\Omega}\) zastąpimy źródłem prądowym o rezystancji wewnętrznej \(4\,\mathrm{\Omega}\). To jaki będzie prąd obliczymy z prawa Ohma:
\[\displaystyle{I=\frac{U}{R}=\frac{20}{4}=5\,\mathrm{A} }\]
Schemat po zmianie:
Etap 2
Dwa rezystory połączone równolegle zastąpimy jednym: \(\displaystyle{\frac{1}{4}+\frac{1}{40}=\frac{11}{40} }\), co daje wynik \(\displaystyle{\frac{40}{11}\,\mathrm{\Omega} }\).
Schemat po zmianie:
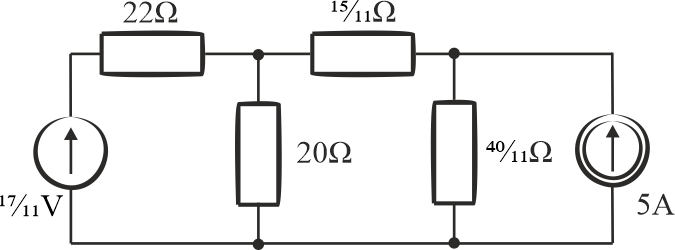
Etap 3
Źródło prądowe o natężeniu prądu \(5\,\mathrm{A}\) i rezystancji wewnętrznej \(\displaystyle{\frac{40}{11}\,\mathrm{\Omega} }\) zastąpimy źródłem napięciowym o rezystancji wewnętrznej \(\displaystyle{\frac{40}{11}\,\mathrm{\Omega} }\). Napięcie wyznaczamy z prawa Ohma:
\[\displaystyle{U=IR=5\cdot\frac{40}{11}=\frac{200}{11}\,\mathrm{V} }\]
Schemat po zmianie:
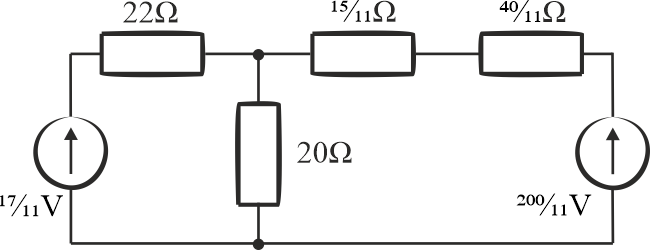
Etap 4
Teraz mamy dwa rezystory połączone szeregowo. Zastąpmy go jednym: \(\displaystyle{\frac{15}{11}+\frac{40}{11}=\frac{55}{11} }\), co daje wynik \(\displaystyle{5\,\mathrm{\Omega} }\).
Schemat po zmianie:
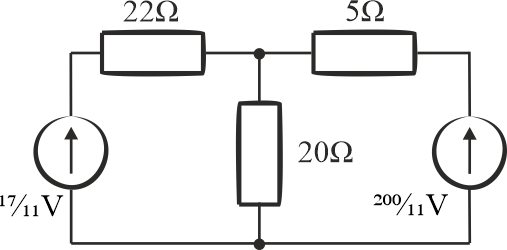
Etap 5
Źródło napięciowe o napięciu \(\displaystyle{\frac{200}{11}\,\mathrm{V}}\) i rezystancji wewnętrznej \(5\,\mathrm{\Omega}\) zastąpimy źródłem prądowym o rezystancji wewnętrznej \(5\,\mathrm{\Omega}\). To jaki będzie prąd obliczymy z prawa Ohma: \(\displaystyle{\frac{200}{11}\cdot \frac{1}{5}=\frac{40}{11}\,\mathrm{A} }\).
Schemat po zmianie:
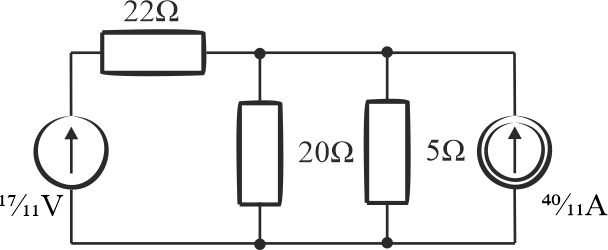
Etap 6
Dwa rezystory połączone równolegle zastąpimy jednym: \(\displaystyle{\frac{1}{20}+\frac{1}{5}=\frac{5}{20} }\), co daje wynik \(\displaystyle{4\,\mathrm{\Omega} }\).
Schemat po zmianie:
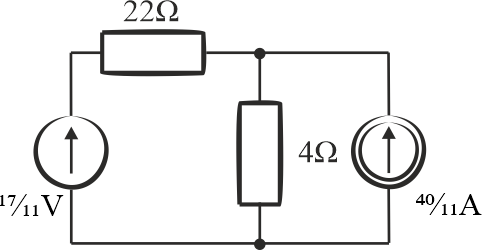
Etap 7
Źródło prądowe o natężeniu prądu \(\displaystyle{\frac{40}{11}\,\mathrm{A}}\) i rezystancji wewnętrznej \(\displaystyle{4\,\mathrm{\Omega} }\) zastąpimy źródłem napięciowym o rezystancji wewnętrznej \(\displaystyle{4\,\mathrm{\Omega} }\). Napięcie wyznaczamy z prawa Ohma: \(\displaystyle{U=4\cdot\frac{40}{11}=\frac{160}{11}\,\mathrm{V} }\)
Schemat po zmianie:
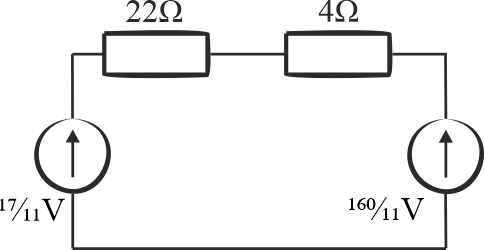
Prąd płynący w tym obwodzie obliczamy z prawa Ohma:
\[\displaystyle{I=\frac{\frac{160}{11}\,\mathrm{V} -\frac{17}{11}\,\mathrm{V}}{22\,\mathrm{\Omega}+4\,\mathrm{\Omega}}=\frac{1}{2}\,\mathrm{A} }\]
Minus w liczniku oznacza, że jedno ze źródeł napięciowych skierowane jest przeciwnie do kierunku prądu. Kierunek prądu jest taki jak źródła o większej wartości napięcia (źródło po prawej).
Odpowiedź
Natężenie prądu wynosi \(I=0,5\,\mathrm{A}\).
