7.2.1.3
Załóż, że bateria może składać się z ogniw połączonych według poniższego schematu.
Wskazówka teoretyczna
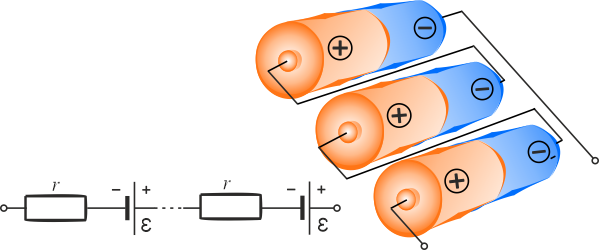
W połączeniu szeregowym jednakowych ogniw sumują się ich rezystancje wewnętrzna \(r\) oraz SEM \(\varepsilon\).
\(\displaystyle{r_w=\sum_{i=1}^{n}r_i}\) oraz \(\displaystyle{\varepsilon_w=\sum_{i=1}^{n}\varepsilon_i}\)
W połączeniu szeregowe \(n\) jednakowych akumulatorów pojemności jest taka jak pojedynczego ogniwa.
Łączenie równoległe ogniw.
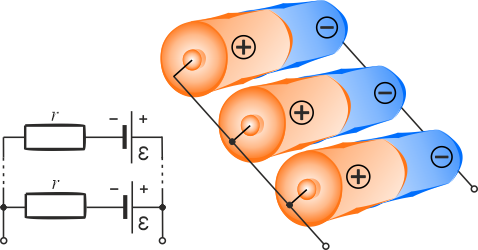
W połączeniu równoległym \(n\) jednakowych ogniw, rezystancja wewnętrzna malej: \(\displaystyle{r_w=\frac{r}{n} }\), a napięcie jest takie jak pojedynczego ogniwa. Przy połączeniu równoległym akumulatorów sumują się pojemności - pojemność wzrasta, np. jeżeli połączymy w szereg dwa akumulatory o pojemności \(1800\,\mathrm{Ah}\), uzyskamy w sumie akumulator o pojemności \(3600\,\mathrm{Ah}\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- ilość ogniw \(N=25\),
- SEM ogniw \(\varepsilon=3\,\mathrm{V}\),
- opór wewnętrzny ogniw \(r=10\,\mathrm{\Omega}\),
- rezystancja obciążenia \(R=10\,\mathrm{\Omega}\).
Szukane:
- prąd po podłączeniu odbiornika \(R\): \(I\).
Analiza sytuacji
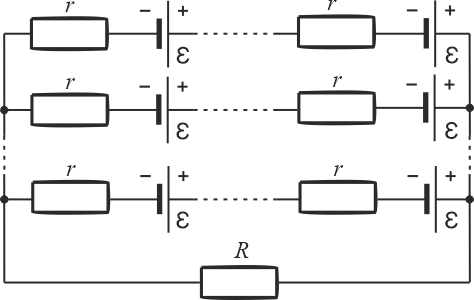
W przypadku tym występuje połączenie mieszane. Mamy ogniwa połączone w szeregu i równolegle. Załóżmy, że bateria będzie składać się z \(m\) szeregów połączonych równolegle, przy czym każdy szereg będzie zawierał \(n\) ogniw połączonych szeregowo. Do dyspozycji mamy \(N=25\) ogniw, czyli \(N=n\cdot m\).
Każdy szereg będzie miał SEM \(E_{sz}=\varepsilon\cdot n\) oraz opór wewnętrzny \(R_{sz}=n\cdot r\)
Ponieważ szeregi te są połączone ze sobą równolegle, więc wypadkowa SEM całej baterii \(E_w=E_{sz}\) będzie wynosić \(E_w=\varepsilon\cdot n\), natomiast wypadkowy opór wewnętrzny całej baterii będzie równy
\[\displaystyle{R_w=\frac{R_{sz}}{m}=\frac{nr}{m} }\]
W obwodzie będzie płynął prąd
\[\displaystyle{I=\frac{E_w}{R_w+R}=\frac{n\varepsilon}{\frac{nr}{m}+R} }\]
Maksymalny pobór mocy będzie wtedy gdy rezystancja wewnętrzna źródła będzie równa rezystancji obciążenia (obliczenia na temat maksymalnej mocy znajdują się w zadaniu 7.2.2.2). Można więc zapisać
\[\displaystyle{R=\frac{nr}{m} }\]
Wiedząc, że \(nm=N\) otrzymujemy
\[\displaystyle{R=\frac{\frac{N}{m}r}{m} }\]
stąd
\[\displaystyle{m=\sqrt{\frac{Nr}{R}} }\]
Rozwiązanie
Ilość szeregów obliczamy następująco
\[\displaystyle{m=\sqrt{\frac{Nr}{R}}=\sqrt{\frac{25\cdot 10}{10}}=5 }\]
Ilość gałęzi wynosi \(\displaystyle{n=\frac{N}{m}=\frac{25}{5}=5 }\)
Prąd płynący w obwodzie wynosi
\[\displaystyle{I=\frac{n\varepsilon}{\frac{nr}{m}+R}=\frac{5\cdot 3}{\frac{5\cdot 10}{5}+10}=\frac{3}{4}\,\mathrm{A} }\]
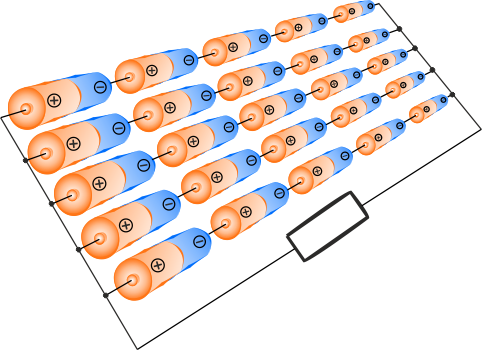
Ogniwa należy połączyć po \(5\) w szeregu. Takich szeregów mamy też pięć.
Odpowiedź
Ogniwa należy połączyć w pięć szeregów połączonych równolegle po 5 ogniw w każdym szeregu. Po podłączeniu obciążenia o rezystancji \(R\) w obwodzie popłynie prąd o wartości \(0,75\,\mathrm{A}\).
