Zadanie 7.2.1.4
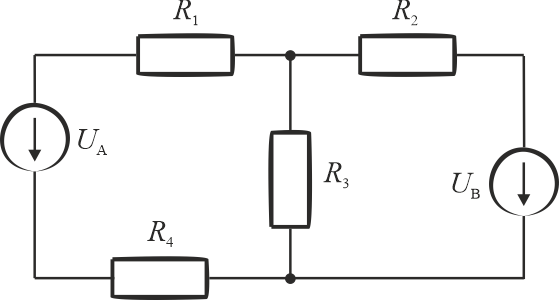
Dane: \(R_1=R_4=100\,\mathrm{\Omega}\), \(R_2=R_3=400\,\mathrm{\Omega}\), \(U_A=20\,\mathrm{V}\), \(U_B=4\,\mathrm{V}\).
Wskazówka teoretyczna
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wartości rezystancji:\(R_1=R_4=100\,\mathrm{\Omega}\), \(R_2=R_3=400\,\mathrm{\Omega}\),
- napięcia źródeł: \(U_A=20\,\mathrm{V}\), \(U_B=4\,\mathrm{V}\).
Szukane:
- prądy: \(I_1\), \(I_2\), \(I_3\).
Analiza sytuacji
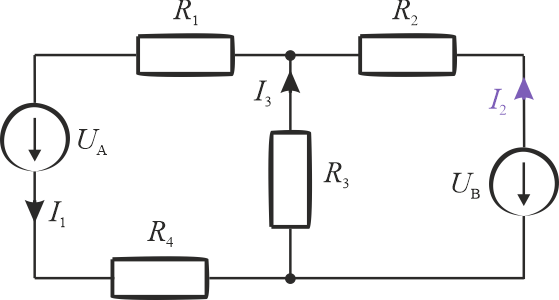
Rozwiązanie zadania zacznijmy od narysowania kierunków płynących prąd. W układzie mamy dwa źródła. Załóżmy, że wymuszają one kierunek prądu w gałęzi w której się znajdują. Oba źródła wymuszają prądy płynące "w dół schematu" - w stronę węzła między rezystorami \(R_3\) i \(R_4\). W zasadzie to w takim przypadku dwa prądy wpływają do węzła więc według I prawa Kirchhoffa prąd płynący przez rezystor \(R_3\) musi wypływać z tego węzła. W taki sposób określiliśmy wstępnie kierunki płynięcia prądów w układzie. Założone kierunki mogą być inne niż w rzeczywistości. To jak płyną prądy w tym układzie dowiemy się na koniec obliczeń. Jeżeli nieprawidłowo określimy kierunek płynięcia prądu to w obliczeniach otrzymamy wartość ujemną tego prądu.
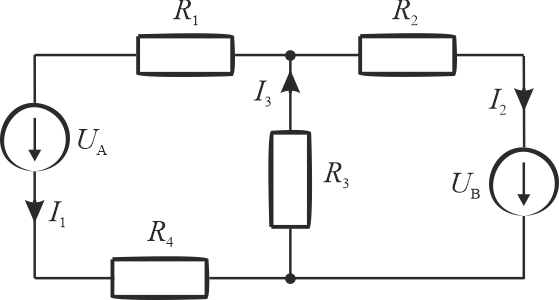
Z I prawa Kirchhoffa, dla obu węzłów mamy to samo równanie:
\[I_1+I_2=I_3\]
Metoda superpozycji wymaga podzielenia schematu na tyle ile mamy źródeł w układzie, tak aby za każdym razem było tylko jedno źródło. W tym przypadku będą dwa pomocnicze schematy. W jednym będzie tylko źródło \(U_A\), w drugim tylko źródło \(U_B\).
Rozwiązanie - układ A
Po usunięciu ze schematu źródła \(U_B\) na nowo określamy kierunki płynięcia prądów. Kierunki te pokazane są na poniższym schemacie.
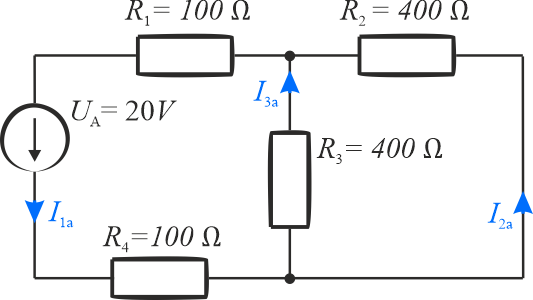
I prawo Kirchhoffa będzie miało postać: \(I_{1a}=I_{2a}+I_{3a}\)
W następnym kroku wyznaczamy rezystancję zastępczą tego układu
\[\displaystyle{R_{za}=R_1+R_4+\frac{R_2\cdot R_3}{R_2+R_3} }\]
\[\displaystyle{R_{za}=100+100+\frac{400\cdot 400}{400+400}=400\,\mathrm{\Omega} }\]
Prąd \(I_{1a}\) będzie płyną przez rezystancję zastępczą \(R_{za}\), więc z prawa Ohma mamy \(\displaystyle{I_{1a}=\frac{U_A}{R_{za}} }\)
\[\displaystyle{I_{1a}=\frac{20}{400}=0,05\,\mathrm{A} }\]
Rezystory \(R_2\) oraz \(R_3\) połączone są równolegle, więc \(U_2=U_3\) i dalej
\[I_{3a}\cdot R_3=I_{2a}\cdot R_2\]
Wartości rezystancji \(R_2\) oraz \(R_3\) są takie same, więc w tym przypadku \(I_{3a}=I_{2a}\)
Wracając do I prawa Kirchhoffa możemy zapisać \(I_{1a}=I_{2a}+I_{3a}=2I_{2a}\) i stąd \(I_{2a}=I_{1a}\cdot 0,5=0,025\,\mathrm{A}\).
Wartości prądów są następujące
\[\left\{\begin{matrix} I_{1a}=0,05\,\mathrm{A} \\ I_{2a}=0,025\,\mathrm{A} \\ I_{3a}=0,025\,\mathrm{A} \end{matrix}\right.\]
Rozwiązanie - układ B
Po usunięciu ze schematu źródła \(U_A\) na nowo określamy kierunki płynięcia prądów. Kierunki te pokazane są na poniższym schemacie.
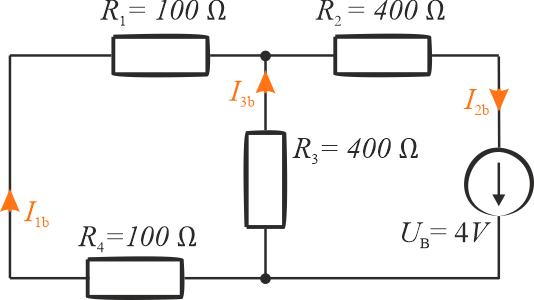
I prawo Kirchhoffa będzie miało postać: \(I_{2ba}=I_{1b}+I_{3b}\)
W następnym kroku wyznaczamy rezystancję zastępczą tego układu
\[\displaystyle{R_{zb}=R_2+\frac{\left (R_1+R_4\right )\cdot R_3}{R_1+R_4+R_3} }\]
\[\displaystyle{R_{zb}=400+\frac{\left (100+100\right )\cdot 400}{100+100+400}=\frac{1600}{3}\,\mathrm{\Omega} }\]
Prąd \(I_{2b}\) będzie płyną przez rezystancję zastępczą \(R_{zb}\), więc z prawa Ohma mamy \(\displaystyle{I_{2b}=\frac{U_B}{R_{zb}} }\)
\[\displaystyle{I_{2b}=\frac{4}{\frac{1600}{3}}=0,0075\,\mathrm{A} }\]
Rezystory \(R_1\) i \(R_4\) połączone są szeregowo, można więc zastąpić je jednym \(R_{14}=R_1+R_4\). Rezystor \(R_{14}\) oraz \(R_3\) połączone są równolegle, więc \(U_{14}=U_3\) i dalej
\[\begin{matrix} I_{1b}\cdot R_{14}=I_{3b}\cdot R_3\\ I_{1b}\cdot 200=I_{3b}\cdot 400 \\ I_{1b}=2\cdot I_{3b} \end{matrix}\]
Wracając do I prawa Kirchhoffa możemy zapisać \(I_{2b}=I_{1b}+I_{3b}=2I_{3b}+I_{3b}=3I_{3b}\) i stąd \(I_{3b}=I_{2b}\cdot \frac{1}{3}=0,0025\,\mathrm{A}\).
Wartości prądów są następujące
\[\left\{\begin{matrix} I_{1b}=0,005\,\mathrm{A} \\ I_{2b}=0,0075\,\mathrm{A} \\ I_{3b}=0,0025\,\mathrm{A} \end{matrix}\right.\]
Rozwiązanie
Kierunki i wartości prądów płynących w układzie \(A\) oraz \(B\) pomogą nam obliczyć natężenie prądów: \(I_1\), \(I_2\) oraz \(I_3\) płynących w układzie. Prąd płynący w gałęzi pierwszej \(I_1\) skierowany jest w dół, tak jak prąd w tej samej gałęzi w układzie \(A\). Prąd płynący zaś w układzie \(B\) jest skierowany ku górze. Widać, że prądy wymuszone przez różne źródła są skierowane przeciwnie. Sumując je musimy temu przeciwnie skierowanemu do \(I_1\) przypisać znak minus. Równanie dla tej gałęzi ma postać \(I_1=I_{1a}-I_{1b}\). Podobnie postępujemy dla kolejnych gałęzi:
\[\left\{\begin{matrix} I_1=I_{1a}-I_{1b}\\ I_2=I_{2b}-I_{2a} \\ I_3=I_{3a}+I_{3b} \end{matrix}\right.\]
\[\left\{\begin{matrix} I_1=0,05-0,005=0,045\,\mathrm{A}\\ I_2=0,0075-0,025=-0,0175 \,\mathrm{A}\\ I_3=0,025+0,0025=0,0275 \,\mathrm{A}\end{matrix}\right.\]
Prąd \(I_2\) ma wartość ujemną. Oznacza to, że płynie on w przeciwnym kierunku w stosunku do tego co na początku założyliśmy. Poniżej zaznaczone są kierunku prądów płynących w układzie.
Odpowiedź
Wartości prądów płynących w układzie: \(I_1=45\,\mathrm{mA}\), \(I_2=17,5\,\mathrm{mA}\), \(I_3=27,5\,\mathrm{mA}\).
