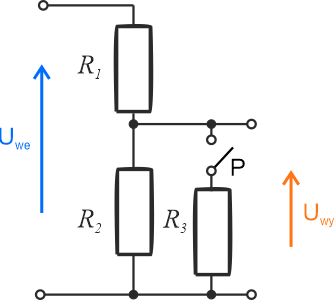
Zadanie 7.2.1.5
a) Ile wynosi napięcie na wyjściu dzielnika?
b) Ile wynosi stosunek napięć \(\displaystyle{\frac{U_{wy}}{U_{we}}}\)?
c) Czy po włączeniu włącznika \(P\) napięcie \(U_{wy}\) ulegnie zmianie? Ile, w takim przypadku, będzie wynosić stosunek \(\displaystyle{\frac{U_{wy}}{U_{we}}}\)?
Wartości elementów: \(R_1 = 200\,\mathrm{\Omega}\), \(R_2 = 100\,\mathrm{\Omega}\), \(R_3 = 100\,\mathrm{\Omega}\).
Wskazówka teoretyczna
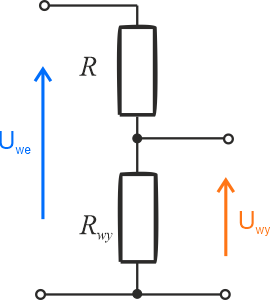
Dla dzielnika przedstawionego na schemacie, stosunku pomiędzy napięciami wynosi:
\[\displaystyle{\frac{U_{wy}}{U_{we}}=\frac{R_{wy}}{R+R_{wy}}}\]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wartości rezystorów: \(R_1 = 200\,\mathrm{\Omega}\), \(R_2 = 100\,\mathrm{\Omega}\), \(R_3 = 100\,\mathrm{\Omega}\),
- napięcie na wejściu dzielnika: \(U_{we}=30\,\mathrm{V}\).
Szukane:
- napięcie na wyjściu dzielnika (gdy w układzie nie jest podłączony rezystor \(R_3\)): \(U_{wy}\),
- stosunek napięć (gdy w układzie nie jest podłączony rezystor \(R_3\)): \(\displaystyle{\frac{U_{wy}}{U_{we}}}\),
- napięcie na wyjściu dzielnika (gdy w układzie jest podłączony rezystor \(R_3\)): \(U_{2wy}\)
- stosunek napięć (gdy w układzie jest podłączony rezystor \(R_3\)): \(\displaystyle{\frac{U_{2wy}}{U_{we}}}\).
Analiza sytuacji
W przypadku, gdy w układzie nie jest podłączony rezystor \(R_3\), prąd płynący w gałęzi, w której mammy rezystory \(R_1\) oraz \(R_2\), wynosi
\[\displaystyle{I=\frac{U_{we}}{R_1+R_2}}\]
Napięcie mierzone na rezystorze \(R_2\) wyniesie \(U_{wy}=I\cdot R_2\), a stąd mamy:
\[\displaystyle{I=\frac{U_{wy}}{R_2}}\]
Możemy zatem zapisać, że
\[\displaystyle{\frac{U_{wy}}{R_2}=\frac{U_{we}}{R_1+R_2}}\]
Napięcie na wyjściu dzielnika możemy obliczyć na podstawie wzoru:
\[\displaystyle{U_{wy}=U_{we}\frac{R_2}{R_1+R_2}}\]
Widzimy, że wyrażenie \(\displaystyle{\frac{R_2}{R_1+R_2}}\) pełni rolę współczynnika od którego zależy to, ile napięcie na wyjściu dzielnika będzie mniejsze od napięciu na wejściu dzielnika.
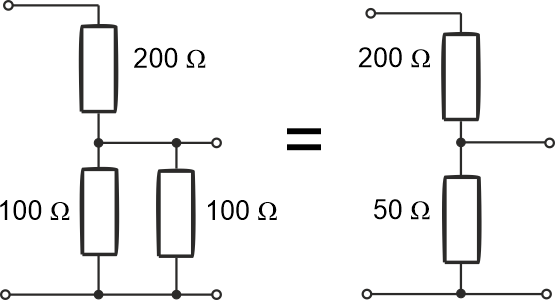
Po włączeniu rezystora \(R_3\) (przełącznika \(P\) włączony) układ dzielnika ulegnie zmianie. W tej sytuacji mamy połączenie równoległe rezystorów \(R_2\) z \(R_3\). Można wyznaczyć rezystancję zastępczą dla tych rezystorów:
\[\displaystyle{R_{23}=\frac{R_2\cdot R_3}{R_2+R_3} }\]
Po podstawieniu wartości liczbowych otrzymujemy: \(\displaystyle{R_{23}=\frac{100\cdot 100}{100+100}=50\,\mathrm{\Omega}}\)
Teraz mamy już standardowy układ dzielnika.
Rozwiązanie
Punkt a)
Napięcie na wyjściu dzielnika (gdy w układzie nie jest podłączony rezystor \(R_3\)) wynosi
\[\displaystyle{U_{wy}=U_{we}\frac{R_2}{R_1+R_2}=30\,\frac{100}{100+200}=30\cdot \frac{1}{3}=10\,\mathrm{V} }\]
Punkt b)
Stosunek napięcia wyjściowego do wejściowego wynosi \(\displaystyle{\frac{U_{wy}}{U_{we}}= \frac{10\,\mathrm{V}}{30\,\mathrm{V}}=\frac{1}{3}}\).
Punkt c)
Po włączeniu \(R_3\), napięcie na wyjściu dzielnika wyniesie
\[\displaystyle{U_{2wy}=U_{we}\frac{R_{23}}{R_1+R_{23}}=30\,\frac{50}{200+50}=30\cdot \frac{1}{5}=6\,\mathrm{V} }\]
Stosunek napięcia wyjściowego do wejściowego wynosi
\[\displaystyle{\frac{U_{2wy}}{U_{we}}= \frac{6\,\mathrm{V}}{30\,\mathrm{V}}=\frac{1}{5}}\]
Jak widzimy napięcie wyjściowe po podłączeniu rezystora \(R_3\) musi ulec zmianie, ponieważ współczynnik podziału napięć zależy ode wartości rezystorów tworzących dzielnik. Przyłączenie równoległe do opornika \(R_2\) opornika \(R_3\) zmienia układ dzielnika. Tak powstały układ jest równoważny sytuacji, w której rezystor \(R_2 = 100\,\mathrm{\Omega}\) zastępujemy rezystorem o oporności \(50\,\mathrm{\Omega}\).
Odpowiedź
Przed podłączeniem rezystora \(R_3\), napięcie na wyjściu dzielnika wynosi \(U_{wy}=10\,\mathrm{V}\), a stosunek napięć: \(\displaystyle{\frac{U_{wy}}{U_{we}}=\frac{1}{3} }\). Po włączeniu włącznika \(P\) napięcie wyjściowe wynosi \(U_{2wy}=6\,\mathrm{V}\), a stosunek napięć: \(\displaystyle{\frac{U_{2wy}}{U_{we}}=\frac{1}{5} }\).