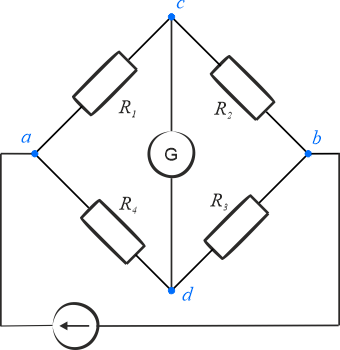
Zadanie 7.2.1.6
  1. Kurs obliczeniowy z fizyki
  2. 7. Elektryczność
  3. 7.2. Obwody prądu stałego
  4. 7.2.1. Nauka
  5. Zadanie 7.2.1.6

 Zadanie 7.2.1.6

Mostek Wheatstone’a
Za pomocą mostka Wheatstone’a zmierzono rezystancję \(R_x\) (przełącznik \(P\) był otwarty). Galwanometr wskazywał stan równowagi, gdy na rezystorze \(R_3\) ustawiona była wartość \(300\,\Omega\).

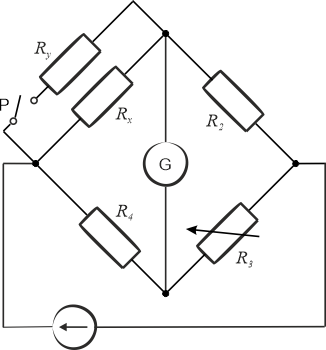
a) Ile wynosi rezystancja rezystora \(R_x\)?
b) Po zmierzeniu rezystancji opornika \(R_x\), do tego rezystora podłączono równolegle rezystor \(R_y\). Tym razem stan równowagi był osiągnięty, gdy wartość rezystora \(R_3\) wynosiła \(600\,\Omega\). Wyznacz rezystancję opornika \(R_y\).

Dane: \(R_2 = 600\,\Omega\), \(R_4 = 200\,\Omega\).

 Wskazówka teoretyczna

 Teoria - równowaga mostka Wheatstone’a
Warunek równowagi dla mostka rezystancyjnego Wheatstone’a jest następujący
\[R_1\cdot R_3=R_2\cdot R_4\]
W takim przypadku galwanometr wskazuje zero, czyli przez środkowy przewód mostka nie płynie prąd.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- \(R_2 = 600\,\Omega\),
- \(R_4 = 200\,\Omega\),
- rezystancja ustawiona na rezystorze \(R_3\) w sytuacji gdy włącznik \(P\) jest otwarty: \(R_{3x}=300\,\Omega\),
- rezystancja ustawiona na rezystorze \(R_3\) w sytuacji gdy włącznik \(P\) jest zamknięty: \(R_{3y}=600\,\Omega\).

Szukane:
- rezystancja rezystora \(R_x\),
- rezystancja rezystora \(R_y\).

Analiza sytuacji

W obydwu sytuacjach mostek zostaje sprowadzony do stanu równowagi, czyli wartość rezystancji na rezystorze \(R_3\) jest dobierana w taki sposób, aby przez gałąź z galwanometrem nie płynął prąd. W takim przypadku iloczyny dwóch rezystancji z naprzeciwległych ramion mostka są takie same, czyli
\[R_x\cdot R_3=R_2\cdot R_4\]

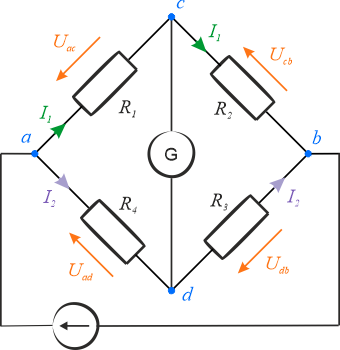
W stanie równowagi przez mostek Wheatstone’a prądy płyną tylko przez gałęzie z rezystorami. W gałęzi z galwanometrem wartość prądu wynosi zero. Na rysunku wprowadzono nazwy węzłów, spadki napięcia na rezystorach oraz prądy.

Prąd \(I\) płynący ze źródła rozpływa się na \(I_1\) oraz \(I_2\), czyli możemy zapisać z I prawa Kirchhoffa
\(\displaystyle{I=I_1+I_2=\frac{U_{ab}}{R_1+R_2}+\frac{U_{ab}}{R_3+R_4} }\)
W stanie równowagi potencjał w węźle \(c\) i \(d\) są takie same, tak więc
\(\displaystyle{U_{cd}=V_c-V_d=U_{cb}-U_{db}=I_1\cdot R_1-I_2\cdot R_3=\frac{U_{ab}}{R_1+R_2}\cdot R_1-\frac{U_{ab}}{R_3+R_4} \cdot R_3}\)

\(\displaystyle{U_{cd}=U_{ab}\left ( \frac{R_1}{R_1+R_2}-\frac{R_3}{R_3+R_4}\right ) }\)

\(\displaystyle{U_{cd}=U_{ab} \frac{R_2R_4-R_3R_1}{(R_1+R_2)(R_3+R_4)} }\)

W równowadze \(U_{cd}=0\). Powyższe wyrażenie jest równe zeru wtedy, gdy licznik będzie równy zeru. I tak otrzymujemy

\(R_2R_4-R_3R_1=0\)

\(R_2R_4=R_3R_1\)

Rozwiązanie

W przypadku a) wartość rezystancji badanej wyznaczamy z zależności:
\[\displaystyle{R_x=\frac{R_2\cdot R_4}{R_{3x}} }\]
\[\displaystyle{R_x=\frac{600\cdot 200}{300}=400\,\Omega }\]

W przypadku b) rezystancji badanej wyznaczamy z zależności:
\[\displaystyle{R_{xy}=\frac{R_2\cdot R_4}{R_{3y}} }\]
\[\displaystyle{R_{xy}=\frac{600\cdot 200}{600}=200\,\Omega }\]

Rezystancja \(R_{xy}\) oznacza rezystancję, jaką uzyskamy po podłączeniu równolegle opornika \(R_x\) i \(R_y\):
\[\displaystyle{R_{xy}=\frac{R_x\cdot R_y}{R_x+R_y} }\]
Po przekształceniach wzoru  \[R_{xy}\cdot R_x+R_{xy}\cdot R_y=R_y\cdot R_x\]\[R_{xy}\cdot R_x=R_y\cdot R_x-R_{xy}\cdot R_y\]\[R_{xy}\cdot R_x=R_y\left (R_x-R_{xy}\right )\]  otrzymujemy zależność
\[\displaystyle{R_y=\frac{R_{xy}\cdot R_x}{R_x-R_{xy}}=\frac{200\cdot 400}{400-200}=400\,\Omega }\]

Odpowiedź

Szukane rezystancje wynoszą: \(R_x=400\,\Omega\), \(R_y=400\,\Omega\).