Zadanie 7.2.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- rezystancja wewnętrzna źródła \(R_w\),
- rezystancja obciążenia \(R\).
Szukane:
- wartość rezystancji odbiornika, przy której wydzieli się na niej maksymalna moc,
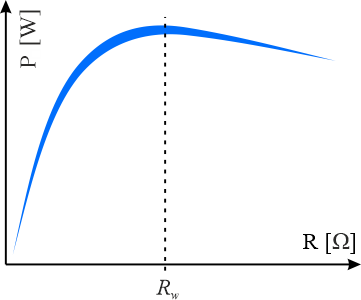
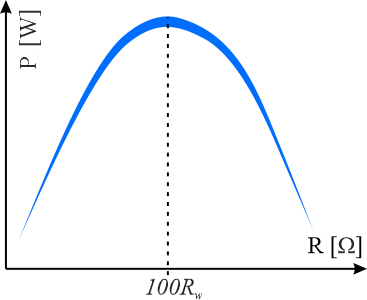
- wykres przedstawiający zależność mocy od rezystancji obciążenia.
Odpowiedź
Maksymalna moc wydzieli się w odbiorniku o rezystancji \(R_w = R\).
Wykres zależność mocy od rezystancji obciążenia.
Polecenie
Dla jakiej wartości rezystancji odbiornika \(R\) wydzieli się na nim maksymalna moc? Wybierz jedno prawidłowe rozwiązanie spośród czterech.
\(R_w=100R\)
\(R_w=2R\)
Rozwiązanie
W obwodzie z rzeczywistym źródłem napięcia (o parametrach \(E\) i \(R_w\)) oraz rezystancją obciążenia \(R\) prąd ma wartość
\[\displaystyle{I=\frac{E}{R_w+R} }\]
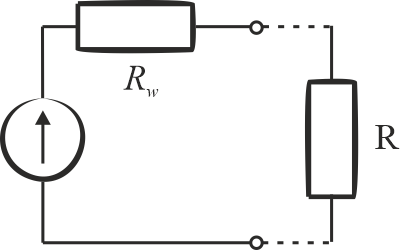
Moc można wyznaczyć z zależności: \(\displaystyle{P=R\cdot I^2=\frac{E^2R}{\left (R_w+R\right )^2} }\)
Aby wyznaczyć maksymalną moc należy policzyć pochodną z mocy po rezystancji:
\[\displaystyle{\frac{\partial P }{\partial R}=\frac{E^2\left ( R_w+R \right )^2-RE^2\cdot 2\left ( R_w+R \right )}{\left ( R_w+R \right )^4}}\]
\[\displaystyle{\frac{\partial P }{\partial R}=\frac{E^2\left ( R_w+R \right )-2RE^2}{\left ( R_w+R \right )^3}}\]
\[\displaystyle{\frac{\partial P }{\partial R}=\frac{E^2\left ( R_w-R \right )}{\left ( R_w+R \right )^3}}\]
Otrzymane wyrażenie jest równe zeru gdy \(R_w=R\). Warto zauważyć, że dla \(R_w = R\) wydzieli się identyczna moc na rezystancji wewnętrznej. Oznacza to, że przy maksymalnym przekazie mocy mamy spore straty energii (równe energii przekazanej do odbiornika).
Polecenie
Sporządź wykres zależności mocy od rezystancji obciążenia. Wybierz jeden prawidłowy spośród dwóch.
Wskazówka: wykorzystaj zależność \(\displaystyle{P=\frac{E^2R}{\left (R_w+R\right )^2} }\)
Odpowiedź
Maksymalna moc wydzieli się w odbiorniku o rezystancji \(R_w = R\).