Zadanie 7.2.2.3
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
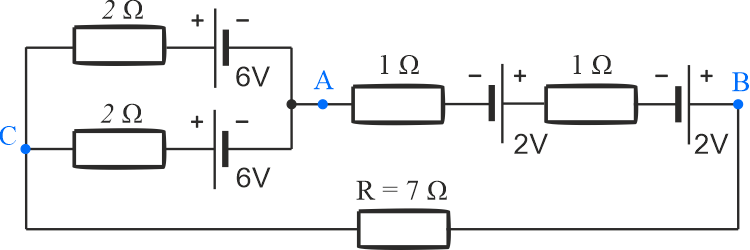
- dwa źródła połączone równolegle: rezystancja wewnętrzna \(r_1=2\,\mathrm{\Omega}\), SEM: \(\varepsilon_1=6\,\mathrm{V}\),
- dwa źródła połączone szeregowo: rezystancja wewnętrzna \(r_2=1\,\mathrm{\Omega}\), SEM: \(\varepsilon_2=2\,\mathrm{V}\),
- rezystancja obciążenie \(R=7\,\mathrm{\Omega}\).
Szukane:
- napięcie między zaciskami \(A\) i \(C\): \(U_{AC}\),
- napięcie między zaciskami \(B\) i \(A\): \(U_{BA}\).
Odpowiedź
Napięcia między odpowiednimi zaciskami wynoszą: \(U_{AC}=5,8\,\mathrm{V}\) oraz \(U_{BA}=-4,4\,\mathrm{V}\).
Polecenie
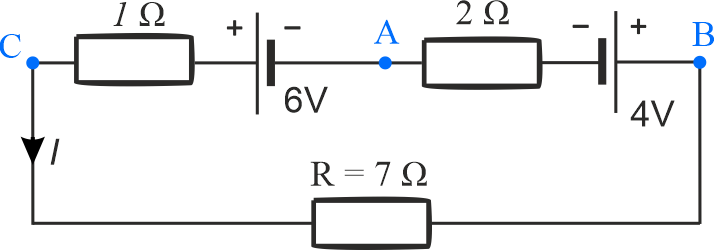
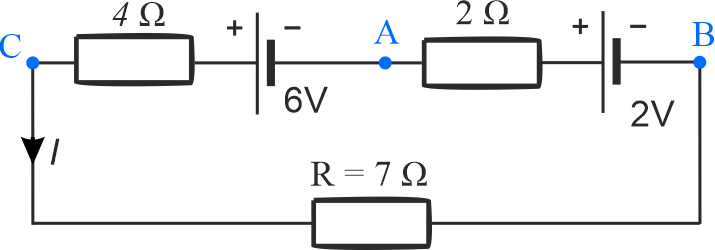
Uprość schemat połączeń do postaci, w której są tylko dwa źródła. Wybierz jeden prawidłowy schemat spośród dwóch.
Nieprawidłowo narysowane źródło drugie oraz błedne wartości \(r_{w1}\) i \(\varepsilon_{w2}\).
Rozwiązanie
Uproszczenie schematu - wyznaczenie jednego źródła z dwóch znajdujących się pomiędzy określonymi zaciskami.
Dwa źródła połączone równolegle między zaciskami \(AC\): rezystancja wypadkowa zastępcza: \(\displaystyle{r_{w1}=\frac{2\cdot 2}{2+2}=1\,\mathrm{\Omega} }\), SEM wypadkowe: \(\varepsilon_{w1}=\varepsilon_1=6\,\mathrm{V}\).
Dwa źródła połączone szeregowomiędzy zaciskami \(AB\): rezystancja wypadkowa zastępcza: \(\displaystyle{r_{w2}=1+1=2\,\mathrm{\Omega} }\), SEM wypadkowe: \(\varepsilon_{w2}=2+2=4\,\mathrm{V}\).
Polecenie
Oblicz napięcie między zaciskami \(U_{AC}\). Wybierz jedną prawidłową wartość spośród czterech.
\(U_{AC}=-6,2\,\mathrm{V}\)
\(U_{AC}=-5,8\,\mathrm{V}\)
Rozwiązanie
Dla całego układu (po uproszczeniu) możemy zapisać II prawo Kirchhoffa
\[\varepsilon_{w1}-\varepsilon_{w2}=Ir_{w1}+Ir_{w2}+IR\]
Z tego równania możemy wyznaczyć prąd płynący w obwodzie
\[\displaystyle{I=\frac{\varepsilon_{w1}-\varepsilon_{w2}}{r_{w1}+r_{w2}+R}=\frac{6-4}{1+2+7}=0,2\,\mathrm{A} }\]
Napięcie między zaciskami \(AC\) wynosi
\[U_{AC}=\varepsilon_{w1}-Ir_{w1}=6-0,2\cdot 1=5,8\,\mathrm{V}\]
Polecenie
Oblicz napięcie między zaciskami \(U_{BA}\). Wybierz jedną prawidłową wartość spośród czterech.
Rozwiązanie
Napięcie między zaciskami \(BA\) wynosi
\[U_{BA}=-\varepsilon_{w2}-Ir_{w2}=-4-0,2\cdot 2=-4,4\,\mathrm{V}\]
Odpowiedź
Napięcia między odpowiednimi zaciskami wynoszą: \(U_{AC}=5,8\,\mathrm{V}\) oraz \(U_{BA}=-4,4\,\mathrm{V}\).