Zadanie 7.2.2.4
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
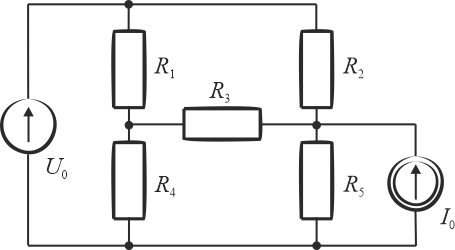
- rezystancje: \(R_1\), \(R_2\), \(R_3\), \(R_4\), \(R_5\),
- napięcie źródła napięciowego: \(U_0\),
- natężenie prądu źródła prądowego: \(I_0\).
Szukane:
- prąd płynący przez rezystor \(R_3\): \(I_{R3}\).
Odpowiedź
Prąd płynący przez rezystor \(R_3\) wynosi \(\displaystyle{I_3=\frac{e_1-e_2}{R_3} }\).
Polecenie
Metoda potencjałów węzłowych jest to metoda w której:
względem węzła odniesienia określane są potencjały pozostałych węzłów.
To nie jest jedyna prawidłowa odpowiedź.
wykorzystywane są prawa Kirchhoffa i prawo Ohma.
To nie jest jedyna prawidłowa odpowiedź.
Rozwiązanie
Metoda potencjałów węzłowych jest jedną z wielu metod wykorzystujących prawa Kirchhoffa i prawo Ohma, przy czym jednak jest najbardziej popularną metodą analizy obwodów elektrycznych, ponieważ najszybciej prowadzi do niezależnego układu równań. W tej metodzie wykonujemy kolejno następujące kroki:
- Wybieramy węzeł odniesienia (którego potencjał przyjmujemy jako zerowy i/lub uziemiony). Względem tego węzła będą określane potencjały innych węzłów. Najlepiej aby węzeł odniesienia łączył możliwie najwięcej elementów (przewodów).
- Oznaczamy symbolami napięcia (np. „\(e_1\)”) pozostałe miejsca obwodu. Do określania prądów stosujemy przewodności \(\displaystyle{G=\frac{1}{R} }\) (lub konduktancje \(\displaystyle{Y=\frac{1}{Z} }\)) mnożone przez różnice napięć, np. \((e_2-e_1)G_2\). Stosujemy prądowe prawo Kirchhoffa do wszystkich węzłów prócz węzła odniesienia (możemy otrzymać \(n-1\) niezależnych równań, gdzie \(n\) - ilość węzłów).
- Rozwiązujemy te równania i uzyskujemy nieznane napięcia węzłów względem węzła odniesienia.
- Obliczamy pozostałe wielkości.
Polecenie
Wskaż prawidłowy układ równań.
\(\left\{\begin{matrix} e_1\left ( G_1+G_3+G_4\right )-e_2G_3=U_0 G_1\\
-e_1G_3+e_2\left ( G_2+G_3+G_5\right )=U_0 G_2+I_0
\end{matrix}\right.\)
\(\left\{\begin{matrix}
e_1\left ( G_1+G_3+G_4\right )-e_2G_3=U_0 G_1\\
e_1G_3+e_2\left ( G_2+G_3+G_5\right )=I_0
\end{matrix}\right.\)
Rozwiązanie
Wybieramy węzeł odniesienia i oznaczamy nieznane napięcia pozostałych węzłów: \(e_1\) i \(e_2\).
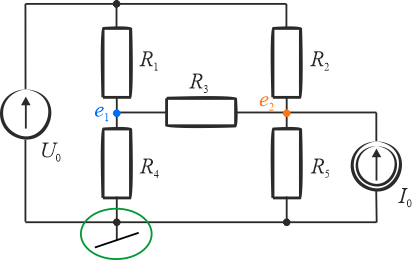
Stosujemy prądowe prawo Kirchhoffa:
- dla węzła \(e_1\): \(\left (e_1-U_0\right ) G_1+\left (e_1-0\right )G_4+\left ( e_1-e_2\right ) G_3=0\)
- dla węzła \(e_2\): \(\left (e_2-U_0\right ) G_1+\left ( e_2-e_1\right ) G_3+\left (e_2-0 \right ) G_5-I_0=0 \)
Polecenie
Prąd płynący przez rezystor \(R_3\) możemy obliczyć z następującego wzoru:
Odpowiedź
Prąd płynący przez rezystor \(R_3\) wynosi \(\displaystyle{I_3=\frac{e_1-e_2}{R_3} }\).
