Zadanie 7.3.1.1
Wskazówka teoretyczna
Pojemność kondensatora płaskiego opisuje zależność:
\[\displaystyle{C=\frac{Q}{\Delta V}=\varepsilon_0 \frac{S}{d} }\]
gdzie \(\varepsilon_0 \) jest przenikalnością elektryczną próżni, \(S\) polem powierzchni okładek kondensatora, \(d\) to odległość między okładkami.
Pojemność kondensatora płaskiego, który wypełniony jest izolatorem, opisuje zależność:
\[\displaystyle{C=\varepsilon_0 \varepsilon \frac{S}{d} }\]
gdzie \(\varepsilon\) jest stałą dielektryczną, która informuje ile razy pojemność danego kondensatora z dielektrykiem jest większa od pojemności kondensatora próżniowego.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- napięcie między okładkami kondensatora \(U=50\,\mathrm{V}\),
- grubość ebonitu \(d=5\,\mathrm{mm}=0,005\,\mathrm{m}\),
- stała dielektryczna \(\varepsilon =3\).
Szukane:
- natężenie pola elektrycznego między okładkami kondensatora po odłączeniu źródła napięcia i usunięciu dielektryka \(E_0\).
Analiza sytuacji
Zajmijmy się najpierw kondensatorem przed odłączeniem go od źródła napięcia i wyciągnięciem izolatora. Pojemność takiego kondensatora wyniesie
\[\displaystyle{C=\frac{Q}{U} }\]
gdzie \(Q\) jest ładunkiem zgromadzonym na okładkach kondensatora, a \(U\) napięciem pomiędzy okładkami. Jest to kondensatora płaski, a więc jego pojemność wynosi
\[\displaystyle{C=\varepsilon_0\, \varepsilon \frac{S}{d} }\]
gdzie \(\varepsilon\) jest stałą dielektryczną substancji między okładkami kondensatora o powierzchni \(S\) odległych od siebie o \(d\).
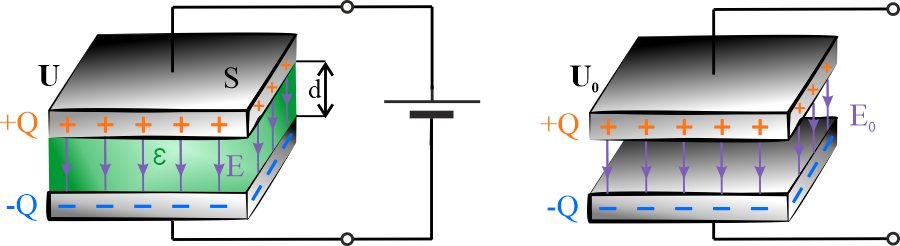
Rysunek. Kondensator z dielektrykiem pomiędzy okładkami podłączony do źródła napięcia (po lewej) oraz kondensator po odłączeniu źródła i usunięciu izolatora (po prawej).
W sytuacji po odłączeniu napięcia i usunięciu dielektryka, obok wymiarów kondensatora, nie ulegnie także zmianie ładunek zgromadzony na jego okładkach. Zakładamy, że okładki kondensatora są izolowane, a więc ładunek nie może przepłynąć między okładką a otoczeniem (między okładkami ładunek także nie przepływa, ponieważ są one odłączone od siebie). Usunięcie dielektryka wpłynie na zmianę pojemności kondensatora, która wyniesie:
\[\displaystyle{C_1=\varepsilon_0 \frac{S}{d} }\]
ponieważ dla powietrza \(\varepsilon=1\).
Po przyrównaniu dwóch wyżej zapisanych zależności na pojemność kondensatora, mamy
- przed wyjęciem dielektryka: \(\displaystyle{\frac{Q}{U} =\varepsilon_0\,\varepsilon \frac{S}{d} }\)
- po wyjęciu dielektryka: \(\displaystyle{\frac{Q}{U_0} =\varepsilon_0 \frac{S}{d} }\)
Napięcie można opisać jako iloczyn pola elektrycznego \(E\) pomiędzy okładkami kondensatora, tak więc po wyjęciu izolatora mamy \(U_0=E_0d\).
Po przekształceniach Równanie I: \[\displaystyle{Q=U\varepsilon_0\,\varepsilon\frac{S}{d}}\] Równanie II: \[\displaystyle{Q=U_0\,\varepsilon_0\frac{S}{d}=E_0\,d\,\varepsilon_0\frac{S}{d}}\]Po przyrówniu ładunków mamy:\[\displaystyle{U\varepsilon_0\,\varepsilon\frac{S}{d}=E_0\,d\,\varepsilon_0\frac{S}{d}}\]\[U\varepsilon=E_0d\] otrzymujemy:
\[\displaystyle{E_0=\varepsilon \frac{U}{d} }\]
Rozwiązanie
Natężenie pola elektrycznego między okładkami kondensatora po odłączeniu źródła napięcia i usunięciu dielektryka, wynosi
\[\displaystyle{E_0=\varepsilon \frac{U}{d}=3\cdot \frac{50}{0,005}=30000\mathrm{\frac{V}{m}} }\]
Odpowiedź
Natężenie pola elektrycznego między okładkami kondensatora po odłączeniu źródła napięcia i usunięciu dielektryka, wynosi \(\displaystyle{E_0=30000\mathrm{\frac{V}{m}} }\).
