Zadanie 7.3.1.2
Wskazówka teoretyczna
W izolowanym układzie ciał całkowity ładunek elektryczny, czyli suma algebraiczna ładunków dodatnich i ujemnych, nie ulega zmianie.
Łączenie równoległe kondensatorów
Jeżeli w układzie jest \(n\) kondensatorów połączonych równolegle, to pojemność zastępczą wyznaczamy przez sumę wszystkich pojemności
\[C_z=\sum_{i=1}^{n}C_i\]
Jeżeli w układzie jest \(n\) kondensatorów połączonych szeregowo, to pojemność zastępczą wyznaczamy przez sumę odwrotności pojemności
\[\displaystyle{\frac{1}{C_z}=\sum_{i=1}^{n}\frac{1}{C_i}}\]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Trochę więcej teorii
1. W połączeniu szeregowym kondensatorów ładunek zgromadzony na każdym kondensatorze jest jednakowy \(Q\). Różnica potencjałów między zaciskami \(ab\) rozkłada się na wszystkie kondensatory, czyli suma spadków napięć na poszczególnych kondensatorach będzie równa napięciu przyłożonemu do zacisków \(ab\).
\[U=U_1+U_2+...+U_n\]
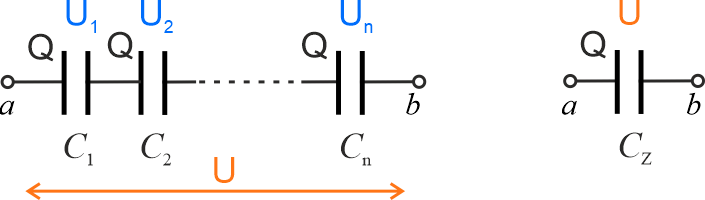
Napięcie na poszczególnych kondensatorach wynosi:
\[\displaystyle{U_i=\frac{Q}{C_i} }\]
Po podstawieniu spadków napięć do pierwszego równania, otrzymujemy:
\[\displaystyle{\frac{Q}{C_Z}=\frac{Q}{C_1}+\frac{Q}{C_1}+...+\frac{Q}{C_n} }\]
Po pomnożeniu równania przez \(Q\) uzyskujemy wzór na pojemność kondensatora zastępczego
\[\displaystyle{\frac{1}{C_Z}=\frac{1}{C_1}+\frac{1}{C_1}+...+\frac{1}{C_n} }\]
2. W łączeniu równoległym \(n\) kondensatorów różnica potencjałów między okładkami każdego z kondensatorów jest jednakowa i wynosi \(U\).
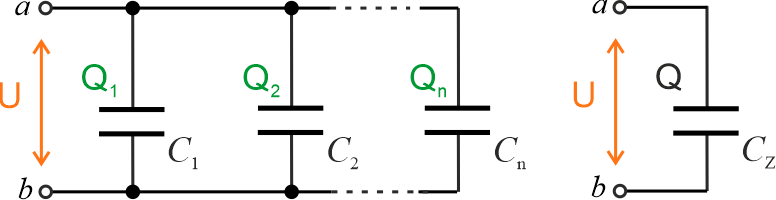
Ładunek zgromadzone na każdym z kondensatorów można wyznaczyć z zależności \(Q_i=UC_i\). Układ kondensatorów możemy zastąpić jednym. Pojemność zastępcza kondensatora musi być tak dobrana, aby po podłączeniu do takiego kondensatora napięcia \(U\), zgromadził się na jego okładkach ładunek \(Q\). Ładunek ten, z prawa zachowania ładunku, wynosi:
\[Q_Z=Q_1+Q_2+...+Q_n\]
\[UC_Z=UC_1+UC_2+...+UC_n\]
Pojemność zastępcza kondensatora wynosi:
\[C_Z=C_1+C_2+...+C_n\]
Dane i szukane
Dane:
- pojemność kondensatora pierwszego \(C_1=2\cdot 10^{-5}\,\mathrm{F} \),
- pojemność kondensatora drugiego \(C_2=1,8\cdot 10^{-4}\,\mathrm{F} \),
- napięcie początkowe na pierwszym kondensatorze \(U_1=100\,\mathrm{V} \).
Szukane:
- napięcie ustalone w układzie po podłączeniu drugiego kondensatora \(U\),
- pojemność zastępcza dwóch kondensatorów połączonych równolegle \(C_r\),
- pojemność zastępcza dwóch kondensatorów połączonych szeregowo \(C_s\).
Analiza sytuacji
Przedstawmy sytuację opisaną w treści zadania na schematach.
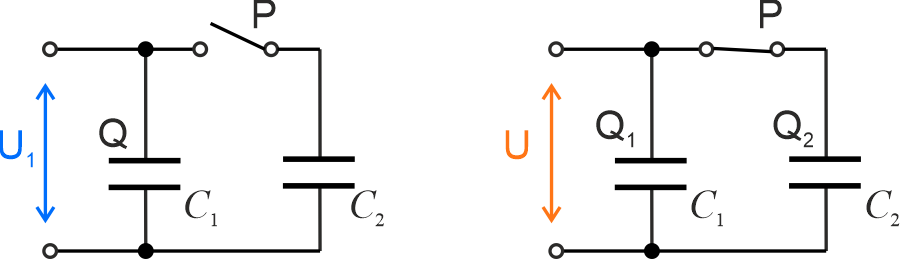
Początkowo kondensator pierwszy o pojemności \(C_1\) naładowany jest do napięcia \(U_1\) zatem ładunek zgromadzony na tym kondensatorze wynosi
\[Q=C_1U_1\]
W chwili podłączenia drugiego kondensatora ładunek \(Q\) zostaje rozdzielony pomiędzy oba kondensatory, czyli
\[Q=Q_1+Q_2\]
W połączeniu równoległym różnica potencjałów na każdym kondensatorze jest taka sama i wynosi \(U\). Można więc zapisać:
\[Q_1=C_1U\]
\[Q_2=C_2U\]
Po podstawieniu równanie określające zachowanie ładunku przybierze postać:
\[C_1U_1=C_1U+C_2U\]
Szukane napięcie wyznaczymy z
\[\displaystyle{U=\frac{C_1}{C_1+C_2}U_1 }\]
Rozwiązanie
Napięcie ustalone w układzie po podłączeniu drugiego kondensatora wynosi
\[\displaystyle{ U=\frac{C_1}{C_1+C_2}U_1 =\frac{2\cdot 10^{-5} }{2\cdot 10^{-5}+1,8\cdot 10^{-4}}\cdot 100=10\,\mathrm{V} }\]
W połączeniu równoległym pojemność kondensatora zastępczego wynosi
\[C_r=C_1+C_2=2\cdot 10^{-5}+1,8\cdot 10^{-4}=2\cdot 10^{-4}\,\mathrm{F}\]
W połączeniu szeregowym pojemność kondensatora zastępczego wynosi
\[\displaystyle{C_s=\frac{C_1\cdot C_2}{C_1+C_2}=\frac{2\cdot 10^{-5}\cdot1,8\cdot 10^{-4}}{2\cdot 10^{-5}+1,8\cdot 10^{-4}}=1,8\cdot 10^{-5}\,\mathrm{F} }\]
Odpowiedź
Napięcie ustalone w układzie po podłączeniu drugiego kondensatora wynosi \(U=10\,\mathrm{V} \). W połączeniu równoległym pojemność kondensatora zastępczego wynosi \(C_r=2\cdot 10^{-4}\,\mathrm{F}\), a w szeregowym \(C_s=1,8\cdot 10^{-5}\,\mathrm{F}\).
