Zadanie 7.3.1.3
a) Ile wynosi energia \(E_0\) zgromadzona w pierwszym kondensatorze przed połączeniem?
b) Ile wynoszą energie \(E_1\) oraz \(E_2\) zgromadzone w pierwszym i drugim kondensatorze po ich połączeniu?
Wskazówka teoretyczna
\[\displaystyle{E_p=\frac{1}{2}CU^2 }\]
gdzie \(C\) jest pojemnością kondensatora naładowanego ładunkiem \(Q\) do napięcia \(U\).
Wyrażenie na energię zgromadzoną przez kondensator może przyjąć również postacie
\[\displaystyle{E_p=\frac{1}{2}QU=\frac{1}{2}\,\frac{Q^2}{C} }\]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- pojemność pierwszego kondensatora \(C_1=20\,\mathrm{\mu F}\),
- pojemność drugiego kondensatora \(C_2=30\,\mathrm{\mu F}\),
- napięcie do jakiego został naładowany kondensator pierwszy \(U_1=100\,\mathrm{V}\).
Szukane:
- energia zgromadzona w pierwszym kondensatorze przed połączeniem \(E_0\),
- energia zgromadzona w pierwszym kondensatorze po ich połączeniu \(E_1\),
- energia zgromadzona w drugim kondensatorze po ich połączeniu \(E_2\).
Rozwiązanie a)
Korzystając z wyrażenia na energię naładowanego kondensatora, możemy policzyć energię zgromadzoną w pierwszym kondensatorze przed połączeniem
\[\displaystyle{E_0=\frac{1}{2}CU^2=\frac{1}{2}\cdot 2\cdot 10^{-5}\cdot 100^2=0,1\,\mathrm{J} }\]
Rozwiązanie b)
Łączenie kondensatorów równoległe powoduje przepływ ładunku z kondensatora pierwszego na drugi aż do wyrównania się napięć na kondensatorach.
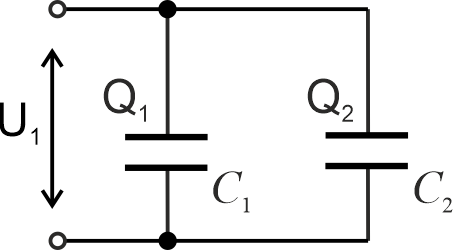
Jeżeli przez \(Q\) oznaczymy ładunek zgromadzony na kondensatorze pierwszym przed połączeniem, a \(Q_1\) i \(Q_2\) - odpowiednio ładunki na obu kondensatorach po połączeniu, możemy zapisać (z zasady zachowania ładunku), że:
\[Q=Q_1+Q_2\]
Poszczególne ładunki wynoszą:
gdzie \(U\) jest napięciem na kondensatorach po podłączeniu.
Ponieważ nie znamy \(U\) możemy z równania drugiego i trzeciego utworzyć jedno:
\[\displaystyle{U=\frac{Q_1}{C_1} }\]
\[\displaystyle{Q_2=C_2\cdot \frac{Q_1}{C_1}=\frac{C_2}{C_1}Q_1 }\]
Wstawiając teraz wyrażenia na \(Q_1\) i \(Q_2\) do równania wynikającego z zasady zachowania ładunku, otrzymujemy:
\[\displaystyle{C_1U_1=Q_1+\frac{C_2}{C_1}Q_1 }\]
Po \[\displaystyle{C_1U_1=Q_1\left ( 1+\frac{C_2}{C_1} \right )}\] \[\displaystyle{Q_1=\frac{C_1U_1}{\frac{C_1+C_2}{C_1}}=\frac{C_1U_1C_1}{C_1+C_2}}\] otrzymujemy
\[\displaystyle{Q_1=\frac{C_1^2U_1}{C_1+C_2} }\]
Podobnie postępując otrzymujemy równanie dla \(Q_2\) \[\displaystyle{Q_1=\frac{C_1}{C_2}Q_2}\] \[\displaystyle{C_1U_1=\frac{C_1}{C_2}Q_2+Q_2}\] \[\displaystyle{C_1U_1=Q_2\left ( \frac{C_1}{C_2}+1\right )}\] \[\displaystyle{Q_2=\frac{C_1U_1}{\frac{C_1+C_2}{C_2}}=\frac{C_1U_1C_2}{C_1+C_2}}\]
\[\displaystyle{Q_2=\frac{C_1C_2U_1}{C_1+C_2} }\]
Skorzystamy ze wzoru na energię naładowanego kondensatora w postaci \(\displaystyle{E=\frac{Q^2}{2C}}\), co dla kondensatora pierwszego i drugiego daje
\[\displaystyle{E_1=\frac{Q_1^2}{2C_1}=\frac{C_1^4U_1^2}{2C_1\left ( C_1+C_2\right )^2} }\]
\[\displaystyle{E_1=\frac{C_1^3U_1^2}{2\left ( C_1+C_2\right )^2}=\frac{\left ( 2\cdot 10^{-5}\right )^3\cdot 100^2}{2\cdot \left (5\cdot 10^{-5}\right )^2}=0,016\,\mathrm{J} }\]
\[\displaystyle{E_2=\frac{Q_2^2}{2C_2}=\frac{C_1^2C_2^2U_1^2}{2C_2\left ( C_1+C_2\right )^2}=\frac{\left (2\cdot 10^{-5}\right )^2\cdot 3\cdot 10^{-5}\cdot 100^2}{2\cdot \left (5\cdot 10^{-5}\right )^2}=0,024\,\mathrm{J} }\]
Oznacza to, że przy połączeniu część energii została stracona wymieniając się na ciepło Joule'a-Lenza przy krótkotrwałym przepływie prądu pomiędzy łączonymi kondensatorami.
Odpowiedź
Energia zgromadzona w pierwszym kondensatorze przed połączeniem wynosi \(E_0=0,1\,\mathrm{J}\). Energie zgromadzone w kondensatorach po ich połączeniu wynoszą: \(E_1=0,016\,\mathrm{J}\) oraz \(E_2=0,024\,\mathrm{J}\).
