Zadanie 7.3.1.5
Wskazówka teoretyczna
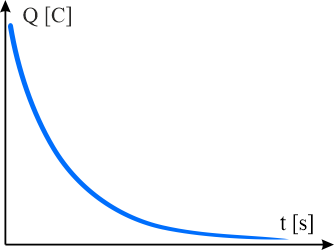
Rozładowanie kondensatora opisuje funkcja
\[\displaystyle{Q(t)=Q_0\cdot \exp{\left (-\frac{t}{\tau }\right )} }\]
gdzie \(Q_0\) - ładunek na kondensatorze, \(\tau = RC\) jest czasem relaksacji, po którym wartość funkcji \(\displaystyle{\exp{\left (-\frac{t}{\tau }\right )} }\) maleje \(e\approx 2,718\) razy.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- pojemność kondensatora \(C=0,02\,\mathrm{\mu F}\),
- rezystancja opornika \(R=2\,\mathrm{M\Omega}\).
Szukane:
- czas w jakim kondensator rozładuje się do połowy \(t\).
Analiza sytuacji
Jeżeli do naładowanego kondensatora dołączymy opornik, zamkniemy obwód i rozpocznie się rozładowywanie kondensatora.
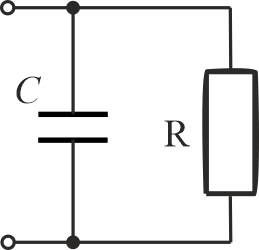
Zgodnie z II prawem Kirchhoffa mamy:
\[\displaystyle{\frac{Q}{C}+IR=0 }\]
\[\displaystyle{\frac{Q}{C}+\frac{\mathrm{d} Q}{\mathrm{d} t}R=0 }\]
Otrzymujemy równanie różniczkowe postaci
\[\displaystyle{\frac{\mathrm{d} Q}{\mathrm{d} t}=-\frac{Q}{RC} }\]
Po rozdzielaniu zmiennych możemy równanie obustronnie scałkować
\[\displaystyle{\int \frac{\mathrm{d} Q}{Q}=-\frac{1}{RC}\int \mathrm{d} t }\]
\[\displaystyle{\int \frac{1}{x}\,\mathrm{d} x= \ln \left | x \right |+C}\] \[\int \mathrm{d} x=x+C\]
Po całkowaniu otrzymujemy (przyjmujemy, że ładunek \(Q>0\)
\[\displaystyle{\ln Q=-\frac{1}{RC}\cdot t+stała }\]
Stałą "stała" wyznaczymy w warunków początkowych, czyli dla \(t=0\) ładunek wynosił \(Q_0\)
\[\displaystyle{\ln Q_0=-\frac{1}{RC}\cdot 0+stała }\]
\[stała = \ln Q_0\]
Otrzymujemy równanie: \(\displaystyle{\ln Q=-\frac{1}{RC}\cdot t+\ln Q_0 }\)
Po skorzystaniu z definicji logarytmu, otrzymujemy:
\[\displaystyle{Q=\exp\left ( -\frac{t}{RC} +\ln Q_0\right )= \exp\left ( -\frac{t}{RC}\right )\exp\left (\ln Q_0\right ) }\]
\[\displaystyle{Q=Q_0\exp\left ( -\frac{t}{RC}\right )}\]
Rozwiązanie
Do równania \(\displaystyle{Q=Q_0\exp\left ( -\frac{t}{RC}\right )}\) podstawiamy dane z treści zadania, czyli \(Q=0,5\cdot Q_0\) - rozładowanie do połowy oznacza, że na okładkach ładunek zmaleje dwukrotnie.
\[\displaystyle{\frac{Q_0}{2}=Q_0\exp\left ( -\frac{t}{RC}\right )}\]
Mnożąc obustronnie równie przez \(Q_0\) oraz logarytmując, mamy
\[\displaystyle{\ln\frac{1}{2}= -\frac{1}{RC}\cdot t }\]
Czas rozładowania do połowy obliczymy z zależności
\[t=RC\cdot (-1)\cdot \ln \frac{1}{2}=RC\cdot \ln 2 \]
\[t=2\cdot 10^6\cdot 0,02\cdot 10^{-6}\cdot \ln 2\approx0,028\,\mathrm{s}\]
Odpowiedź
Czas po jakim kondensator rozładuje się do połowy, wynosi \(t=0,028\,\mathrm{s}\).
