Zadanie 7.3.2.1
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- pojemność dwóch kondensatorów \(C\),
- stała dielektryczna \(\varepsilon=3\).
Szukane:
- pojemność zastępcza dwóch kondensatorów bez dielektryka \(C_1\),
- pojemność zastępcza dwóch kondensatorów, z których jeden jest wypełniony dielektrykiem \(C_2\),
- ładunek zgromadzony przez kondensator zastępczy \(C_1\): \(Q_1\),
- ładunek zgromadzony przez kondensator zastępczy \(C_2\): \(Q_2\).
Odpowiedź
Po włożeniu dielektryka o stałej dielektrycznej \(\varepsilon=3\) do jednego z kondensatorów, pojemność zastępcza oraz zgromadzony ładunek wzrosną dwukrotnie.
Polecenie
O ile zmieniła się pojemność zastępcza układu dwóch kondensatorów po włożeniu dielektryka do jednego z nich? Wybierz jedną prawidłową odpowiedź spośród dwóch.
\(C_1=2C_2\)
\(C_2=2C_1\)
Rozwiązanie
Dwa kondensatory połączone równolegle można zastąpić jednym. W tym celu dodajemy ich pojemności.
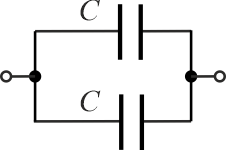
\[C_1=C+C=2C\]
Po tym jak włożono do jednego z kondensatorów ebonit, sytuacja wygląda następująco:

Stała dielektryczna ma wartość \(3\), dlatego pojemność kondensatora z dielektrykiem wzrośnie trzykrotnie. Tym razem pojemność zastępcza wynosi
\[C_2=C+3C=4C\]
Aby wyznaczyć o ile zmieniła się pojemność zastępcza układu dwóch kondensatorów, liczymy stosunek ich pojemności zastępczych.
\[\displaystyle{\frac{C_1}{C_2}=\frac{2C}{4C}=\frac{1}{2} }\]
\[2C_1=C_2\]
Polecenie
Czy zmieni się ilość ładunku gromadzonego na kondensatorze zastępczym w wymienionych dwóch przypadkach? Jeśli tak to o ile? Wybierz jedną prawidłową odpowiedź spośród trzech.
Tak. Ładunek wynosi
Tak. Ładunek wynosi
Nie. Ładunek wynosi
Rozwiązanie
Ładunki na kondensatorach zastępczych \(C_1\) oraz \(C_2\) wynoszą
Napięcie \(U\) jest takie samo, ponieważ zakładamy, że podłączamy kondensatory do tego samego źródła napięcia.
Stosunek pojemności wynosi
\[\displaystyle{\frac{Q_1}{Q_2}=\frac{2CU}{4CU}=\frac{1}{2} }\]
\[Q_2=2Q_1\]
Odpowiedź
Po włożeniu dielektryka o stałej dielektrycznej \(\varepsilon=3\) do jednego z kondensatorów, pojemność zastępcza oraz zgromadzony ładunek wzrosną dwukrotnie.
