Zadanie 7.3.2.2
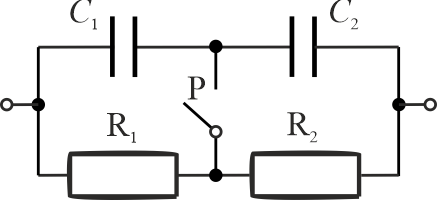
- Ile wynosi napięcie zasilające, jeżeli wiadomo, że \(R_1=R_2\). Spadek napięcia na rezystorze \(R_2\) wynosi \(4\,\mathrm{V}\)? Przełącznik \(P\) jest otwarty.
- Ile wynoszą napięcia na kondensatorach? Przełącznik \(P\) jest otwarty.
- Ile wynoszą napięcia na kondensatorach, jeżeli zamkniemy przełącznik \(P\)?
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- spadek napięcia na rezystorze \(R_2\): \(U_{R2}=4\,\mathrm{V}\),
- pojemności kondensatorów \(C_1=30\,\mathrm{\mu F}\), \(C_2=15\,\mathrm{\mu F}\),
- rezystancje \(R_1=R_2\).
Szukane:
- napięcia zasilające \(U\),
- napięcia na kondensatorach, gdy przełącznik \(P\) jest otwarty: \(Uo_{C1}\), \(Uo_{C2}\),
- napięcia na kondensatorach, gdy przełącznik \(P\) jest zamknięty: \(Uz_{C1}\), \(Uz_{C2}\).
Odpowiedź
Napięcie zasilające wynosi \(8\,\mathrm{V}\). Napięcia na kondensatorach w przypadku otwartego przełącznika \(P\) mają wartości \(Uo_{C1}=2,67\,\mathrm{V}\) oraz \(Uo_{C2}=5,33\,\mathrm{V}\). Po zamknięciu przełącznika, a pamiętamy, że źródło jest cały czas włączone, napięcia na obu kondensatorach będą takie same \(Uz_{C1}=Uz_{C2}=4\,\mathrm{V}\).
Polecenie
Ile wynosi napięcie zasilające w przypadku wyłączonego przełącznika \(P\)? Wybierz jedną prawidłową wartość spośród trzech.
\(U=2\,\mathrm{V}\)
Rozwiązanie
Po podłączeniu źródła do zacisków układu w stanie ustalonym przez rezystory \(R_1\) i \(R_2\) popłynie taki sam prąd \(I\). Dla oczka zawierającego te dwa rezystory i źródło możemy zapisać prawo Kirchhoffa
\[U=IR_1+IR_2\] ponieważ \(R_1=R_2\) mamy
\[U=2\cdot IR=2\cdot 4\,\mathrm{V}=8\,\mathrm{V}\]
Polecenie
Ile wynoszą napięcia na kondensatorach, jeżeli przełącznik \(P\) jest otwarty? Wybierz jeden prawidłowy zestaw odpowiedzi.
\(Uo_{C1}=4\,\mathrm{V}\)
\(Uo_{C2}=4\,\mathrm{V}\)
\(Uo_{C1}=2,67\,\mathrm{V}\)
\(Uo_{C2}=5,33\,\mathrm{V}\)
Rozwiązanie
W przypadku, gdy przełącznik \(P\) jest otwarty, kondensatory połączone są szeregowo. Pojemność zastępcza wynosi
\[\displaystyle{C_{12}=\frac{C_1\cdot C_2}{C_1+C_2}=\frac{30\cdot 10^{-6}\cdot 15\cdot 10^{-6}}{(30+15)\cdot 10^{-6}}=10\,\mathrm{\mu F} }\]
Ładunek zgromadzony na kondensatorze zastępczym wynosi
\[Q=U\cdot C_{12}=8 \cdot 10\cdot 10^{-6}=80\,\mathrm{\mu C} \]
Przy połaczeniu szeregowym kondensatorów na każdym z nich ładunek jest ten sam. Napięcia na kondensatorach wynoszą więc
\[Uo_{C1}=\frac{Q}{C_1}=\frac{80\,\mathrm{\mu C}}{30\,\mathrm{\mu F}}=2\frac{2}{3}\,\mathrm{V}\]
\[Uo_{C2}=\frac{Q}{C_2}=\frac{80\,\mathrm{\mu C}}{15\,\mathrm{\mu F}}=5\frac{1}{3}\,\mathrm{V}\]
Polecenie
Ile wynoszą napięcia na kondensatorach, jeżeli przełącznik \(P\) jest zamknięty? Wybierz jeden prawidłowy zestaw odpowiedzi.
\(Uz_{C2}=4\,\mathrm{V}\)
\(Uz_{C2}=5,33\,\mathrm{V}\)
Rozwiązanie
Po zamknięciu przełącznika kondensator \(C_1\) połączony jest równolegle z \(R_1\). To samo mamy dla drugiego kondensatora \(C_2\) oraz rezystora \(R_2\). Wynika stąd, że spadek napięcia na rezystorze jest taki sam jak spadek napięcia na kondensatorze. Ponieważ \(R_1=R_2\), więc spadki napięcia na rezystorach są takie same i wynoszą po \(4\,\mathrm{V}\).
Odpowiedź
Napięcie zasilające wynosi \(8\,\mathrm{V}\). Napięcia na kondensatorach w przypadku otwartego przełącznika \(P\) mają wartości \(Uo_{C1}=2,67\,\mathrm{V}\) oraz \(Uo_{C2}=5,33\,\mathrm{V}\). Po zamknięciu przełącznika, a pamiętamy, że źródło jest cały czas włączone, napięcia na obu kondensatorach będą takie same \(Uz_{C1}=Uz_{C2}=4\,\mathrm{V}\).
