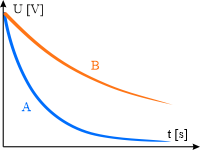
Zadanie 7.3.2.5
  1. Kurs obliczeniowy z fizyki
  2. 7. Elektryczność
  3. 7.3. Kondensator w obwodach prądu stałego
  4. 7.3.2. Trening
  5. Zadanie 7.3.2.5

 Zadanie 7.3.2.5

Ładowanie kondensatora
Wyznacz przebiegi czasowe napięcia ładowania dla dwóch różnych kondensatorów, gdy do układu podłączone jest źródło napięcia stałego \(E\). Pojemności kondensatorów wynoszą \(C\) oraz \(3C\), wartość rezystancji nie zmienia się i wynosi \(R\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- napięcia zasilające \(E\),
- pojemności kondensatorów \(C\) oraz \(3C\),
- rezystancja \(R\).

Szukane:
- wzór opisujący przebieg czasowy napięcia ładowania kondensatora oraz krzywe ładowania.

Odpowiedź

Zależność od czasu określającą zmiany napięcia podczas ładowania kondensatora ma postać \(\displaystyle{U_C(t)=E\left ( 1-e^{-\frac{t}{RC}}\right ) }\).
Charakterystyki dla rożnych stałych czasowych przedstawiono poniżej



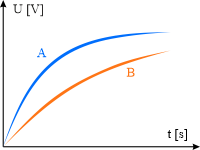
Przebieg \(A\) został narysowany dla stałej czasowej \(RC\), natomiast przebieg \(B\) - dla stałej czasowej \(R\cdot 3C\).

Polecenie

Wyznacz zależność od czasu określającą zmiany napięcia podczas ładowania kondensatora. Wybierz jedno prawidłowe równanie spośród dwóch.

Wybór 1 z 2

\(\displaystyle{U_C=E\left ( 1-e^{-\frac{t}{RC}}\right ) }\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(\displaystyle{U_C=E\cdot e^{-\frac{t}{RC}} }\)

Odpowiedź nieprawidłowa

Rozwiązanie

Wychodząc z II prawa Kirchhoffa mamy

\(\displaystyle{E=U_R+U_C=IR+U_C }\)
\(\displaystyle{E-U_C=\frac{\mathrm{d}Q}{\mathrm{d}t}\cdot R}\)

Za \(Q\) podstawiamy \(Q=U_C\cdot C\) i otrzymujemy

\(\displaystyle{E-U_C=RC\frac{\mathrm{d}U_C}{\mathrm{d}t} }\)
\(\displaystyle{ \frac{\mathrm{d}U_c }{E-U_C}=\frac{1}{RC} \mathrm{d} t }\)

Całkując obustronnie mamy
\(\displaystyle{\int \frac{\mathrm{d}U_c }{E-U_C}=\frac{1}{RC}\int \mathrm{d} t }\)
\(\displaystyle{-\ln\left | E-U_C \right |=\frac{t}{RC}+K }\)

Stałą całkowania \(K\) wyznaczymy dla \(t=0\) i \(U_C=0\) i otrzymujemy  \(\displaystyle{-\ln\left | E-0 \right |=\frac{0}{RC}+K }\)   czyli \(K=-\ln(E)\)

\(\displaystyle{-\ln\left | E-U_C \right |=\frac{t}{RC}-\ln(E) }\)
\(\displaystyle{\ln\left ( E-U_C \right )-\ln(E)=-\frac{t}{RC} }\)
\(\displaystyle{\ln\frac{E-U_C }{E}=-\frac{t}{RC} }\)
\(\displaystyle{\exp\left ( \ln\frac{E-U_C }{E} \right )=\exp\left ( -\frac{t}{RC} \right ) }\)
\(\displaystyle{E-U_C=E\cdot \exp\left ( -\frac{t}{RC} \right ) }\)
\(\displaystyle{U_C=E\left ( 1-e^{-\frac{t}{RC}}\right ) }\)

Polecenie

Wybierz prawidłowy zestaw charakterystyk ładowania kondensatorów spośród trzech przedstawionych poniżej.
 Do wzoru \(\displaystyle{U_C(t)=E\left ( 1-e^{-\frac{t}{RC}}\right ) }\) należy podstawić za pojemność kondensatora drugim razem wartość trzykrotnie większej pojemności. 

Przebieg niebieski oznaczony literką \(A\) został narysowany dla stałej czasowej \(RC\).
Przebieg pomarańczowy oznaczony literką \(B\) został narysowany dla stałej czasowej \(R\cdot 3C\).

Wybór 1 z 3

Odpowiedź prawidłowa

Wybór 2 z 3

Odpowiedź nieprawidłowa

Wybór 3 z 3

Odpowiedź nieprawidłowa

Odpowiedź

Zależność od czasu określającą zmiany napięcia podczas ładowania kondensatora ma postać \(\displaystyle{U_C(t)=E\left ( 1-e^{-\frac{t}{RC}}\right ) }\).
Charakterystyki dla rożnych stałych czasowych przedstawiono poniżej



Przebieg \(A\) został narysowany dla stałej czasowej \(RC\), natomiast przebieg \(B\) - dla stałej czasowej \(R\cdot 3C\).