Zadanie 7.4.1.1
  1. Kurs obliczeniowy z fizyki
  2. 7. Elektryczność
  3. 7.4. Obwody prądu przemiennego i tętniącego
  4. 7.4.1. Nauka
  5. Zadanie 7.4.1.1

 Zadanie 7.4.1.1

Paramety sygnału
Na oscyloskopie zaobserwowano sinusoidalny przebieg napięcia przedstawiony poniżej na rysunku. Ile wynosi amplituda, wartość międzyszczytowa oraz średnia zmierzonego napięcia? Wyznacz częstotliwość tego sygnału. Jakie wartości będą miały wyżej wymienione parametry, jeżeli do danego sygnału sinusoidalnego dodamy napięcie stałe \(6\,\mathrm{V}\)? Pomiar był wykonywany przy następujących ustawieniach  Przyrząd elektroniczny służący do obserwowania napięcia w zależności od czasu.  : podstawa czasu wynosiła \(2\,\mathrm{ms/dz}\), napięcie: \(0,5\,\mathrm{V/dz}\).

 Wskazówka teoretyczna

 Teoria - parametry sygnałów okresowych
Sygnał okresowy zmienny reprezentuje wartość wielkości zmiennej w czasie spełniającą zależność \(x(t)=x(t+kT)\), gdzie \(k=1, 2, ...\), \(T\) - okres sygnału.

Do wielkości (parametrów) charakteryzujących przebiegi okresowe zaliczamy: wartość maksymalną (amplitudę) \(U_m\), wartość średnią \(U_{AV}\), wartość średnią modułu \(U_{\left | AV \right |}\), wartość skuteczną \(U_{RMS}\), wartość międzyszczytową \(U_{p-p}\), okres \(T\), częstotliwość \(f\), współczynnik kształtu \(k_k\) i współczynnik szczytu \(k_{sz}\).

 Przebieg oglądany na oscyloskopie

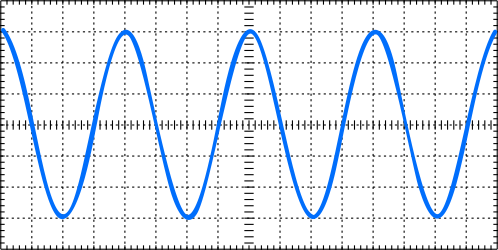
Rysunek
Więcej teorii - parametry
Dla sygnału sinusoidalnego \(u(t)=U_m\sin (\omega t)\) wartość międzyszczytowa jest równa podwojonej amplitudzie \(U_{p-p}=2\cdot U_m\).

Wartość średnią liczymy ze wzoru: \(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{T}u(t)\, dt}\).

Wartość średnią modułu wyznaczamy ze wzoru: \(\displaystyle{U_{\left | AV \right |}=\frac{1}{T}\int_{0}^{T}\left | u(t) \right |\, dt}\).

Wartość skuteczna wynosi \(\displaystyle{U_{RMS}=\sqrt{\frac{1}{T}\int_{0}^{T} u^2(t) \, dt} }\)

Współczynniki kształtu i szczytu wynoszą odpowiednio \(\displaystyle{k_k=\frac{U_{RMS}}{U_{\left | AV \right |}} }\) oraz \(\displaystyle{k_{sz}=\frac{U_{m}}{U_{RMS}} }\)

Więcej teorii - odczyty z oscyloskopu

Mierzymy sygnał okresowy opisany równaniem \(x(t)=X_m\sin(\omega t)\), gdzie \(\displaystyle{\omega=2\pi f=\frac{2\pi}{T} }\). Odczytując okres \(T\) możemy obliczyć częstotliwość \(\displaystyle{f=\frac{1}{T} }\).

Pomiar amplitudy sygnału sinusoidalnego polega na zmierzeniu odległości pomiędzy wielkością maksymalną a minimalną i podzieleniu wyniku przez dwa. 

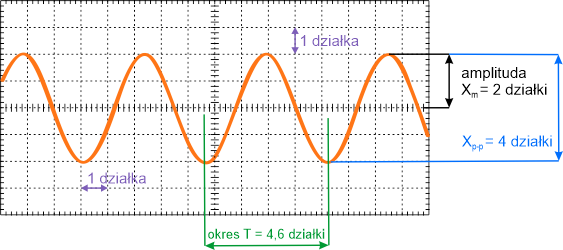
Rysunek


Odczyt działek dokonujemy przy użyciu skali oscyloskopu zaznaczonej przerywanymi liniami. Małe kreski pomagają odczytać części działek. W wielu oscyloskopach przeliczenia odbywają się automatycznie, a urządzenia wyświetlają od razu żądane parametry. Wykonajmy przykładowe przeliczenie dla nastaw podanych w treści zadania (podstawa czasu oraz amplituda).

Okres mierzonego sygnału wynosi \(\displaystyle{T=4,6 \,\mathrm{dz}\cdot 2\cdot 10^{-3}\,\mathrm{\frac{s}{dz}}=9,2\,\mathrm{ms} }\), co daje częstotliwość \(\displaystyle{f=\frac{1}{9,2 \cdot 10^{-3}}=109\,\mathrm{Hz} }\)

Wartość międzyszczytowa napięcia: \(\displaystyle{U_{p-p}=4\,\mathrm{dz}\cdot 0,5\,\mathrm{\frac{V}{dz}}=2\,\mathrm{V} }\)
Napięcie maksymalne wynosi \(U_m=1\,\mathrm{V}\)

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- pomiar amplitudy napięcia: \(0,5\,\mathrm{V/dz}\),
- pomiar okresu: \(2\,\mathrm{ms/dz}\),
- składowa stała sygnału \(U_o=6\,\mathrm{V}\).

Szukane
Parametry bez oraz ze składową stałą:
- amplituda mierzonego napięcia \(U_m\),
- wartość między szczytowa mierzonego napięcia \(U_{p-p}\),
- wartość średnia mierzonego napięcia \(U_{AV}\),
- okres \(T\),
- częstotliwość \(f\).

Pomiary bez składowej stałej

Z pomiaru wykonanego za pomocą oscyloskopu liczymy wartość amplitudy: \(\displaystyle{U_m=3\,\mathrm{dz}\cdot 0,5\,\mathrm{\frac{V}{dz}}=1,5\,\mathrm{V}} \)

Napięcie międzyszczytowe jest w tym przypadku dwa razy większe od amplitudy: \(\displaystyle{U_{p-p}=6\,\mathrm{dz}\cdot 0,5\,\mathrm{\frac{V}{dz}}=3\,\mathrm{V}} \)

Wartość średnia wynosi:

\(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{T} u(t) \, dt=\frac{1}{T}\int_{0}^{T} U_m \sin(\omega t) \, dt }\)
\(\displaystyle{U_{AV}=\frac{U_m}{T}\left [ - \frac{1}{\omega}\cos(\omega t) \right ]^T_0 }\)
\(\displaystyle{U_{AV}=\frac{U_m}{T}\cdot \frac{T}{2\pi}\left ( -\cos\left ( \frac{2\pi}{T}\cdot T \right )+\cos\left ( \frac{2\pi}{T}\cdot 0 \right ) \right )}\)
\(\displaystyle{U_{AV}=\frac{U_m}{2\pi}\cdot (-1+1)=0}\)

 Wartość średnia prądu przemiennego jest równa takiej wartości prądu stałego, która powoduje przepływ takiego samego ładunku w takim samym czasie. 
Okres mierzonego sygnału wynosi \(\displaystyle{T=4 \,\mathrm{dz}\cdot 2\cdot 10^{-3}\,\mathrm{\frac{s}{dz}}=8\,\mathrm{ms} }\), co daje częstotliwość \(\displaystyle{f=\frac{1}{8 \cdot 10^{-3}}=125\,\mathrm{Hz} }\)

wartość średnią z modułu napięcia?


\(\displaystyle{U_{\left | AV \right |}=\frac{1}{T}\int_{0}^{T} \left | u(t) \right | \, dt=\frac{2}{T}\int_{0}^{T/2} U_m \sin(\omega t) \, dt }\) 
\(\displaystyle{U_{\left | AV \right |}=\frac{2U_m}{T}\left [ - \frac{1}{\omega}\cos(\omega t) \right ]^{0,5T}_0 }\)

\(\displaystyle{U_{\left | AV \right |}=\frac{2U_m}{T}\cdot \frac{T}{2\pi}\left ( -\cos\left ( \frac{2\pi}{T}\cdot \frac{T}{2} \right )+\cos\left ( \frac{2\pi}{T}\cdot 0 \right ) \right )}\)

\(\displaystyle{U_{\left | AV \right |}=\frac{U_m}{\pi}\cdot (1+1)=\frac{2}{\pi}\cdot \frac{3}{2} }\)

\(\displaystyle{U_{\left | AV \right |}=\frac{3}{\pi}\,\mathrm{V} }\)

Pomiar ze składową stałą

Dodanie do sygnału sinusoidalnego przemiennego składowej stałej \(U_o\) spowoduje podniesienie funkcji sinus o wartość \(U_o\). Nie zmienią się amplituda napięcia, wartość międzyszczytowa ani okres i częstotliwość. Ulegnie zmianie wartość średnia napięcia.

\(\displaystyle{U2_{AV}=\frac{1}{T}\int_{0}^{T} u(t) \, dt=\frac{1}{T}\int_{0}^{T} \left ( U_m \sin(\omega t)+U_o \right ) \, dt }\)

Tym razem mamy do policzenia dwie całki.

\(\displaystyle{U2_{AV}=\frac{U_m}{T}\left [ - \frac{1}{\omega}\cos(\omega t) \right ]^T_0 +\frac{U_o}{T}\cdot\left [ t \right ]^T_0}\)

Pierwsza całka przyjmuje wartość zero (tak samo jak poprzednio).

\(\displaystyle{U2_{AV}=0+\frac{U_0}{T}\cdot T=U_0 }\)
\(U2_{AV}=6\,\mathrm{V}\)

Odpowiedź

Parametry napięcia sinusoidalnego bez dodanej składowej stałej wynoszą \(U_m=1,5\,\mathrm{V}\), \(U_{p-p}=3\,\mathrm{V}\), \(U_{AV}=0\), \(T=8\,\mathrm{ms}\), \(f=125\,\mathrm{Hz}\). Po dodaniu składowej stałej zmieni się wartość średnia i wyniesie ona \(U2_{AV}=6\,\mathrm{V}\).