Zadanie 7.4.1.2
Wskazówka teoretyczna
\(\displaystyle{U_{RMS}=\sqrt{\frac{1}{T}\int_{0}^{T} u^2(t) \, dt} }\),
gdzie \(T\) - okres. (RMS - Root Mean Square)
Interpretacja fizyczna: wartość skuteczna prądu przemiennego jest równa takiej wartości prądu stałego, która powoduje wydzielenie się na odbiorniku takiej samej energii w takim samym czasie.
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- napięcie maksymalne \(U=2\,\mathrm{V}\) dla obu przebiegów.
Szukane:
- wartość skuteczna dla dwóch przebiegów \(U_{AV}\).
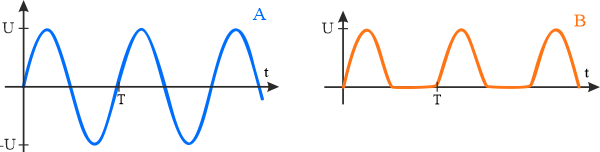
Przebieg \(A\)
Przebieg \(A\) przedstawia sinusoidalną zmianę napięcia w czasie, którą można opisać zależnością \(u(t)=U\sin (\omega t)\). Wartość skuteczną policzymy ze wzoru
\(\displaystyle{U_{RMS}=\sqrt{\frac{1}{T}\int_{0}^{T} U^2\sin^2 (\omega t) \, dt} }\)
Po skorzystaniu ze wzorów
\(\displaystyle{\int b\sin^2 (ax)dx=b\int \frac{1-\cos(2ax)}{2}dx=b\left ( \frac{x}{2}-\frac{1}{2}\cdot \frac{1}{2a}\sin(2ax) \right )+C}\)
mamy
\(\displaystyle{U_{RMS}=\sqrt{\frac{U^2}{T}\left [ \frac{t}{2}-\frac{1}{4\omega}\sin(2\omega t) \right ]^T_0}}\)
\(\displaystyle{U_{RMS}=\frac{U}{\sqrt{T}}\sqrt{\frac{T}{2}-\frac{T}{4\cdot 2\pi}\sin(2\frac{2\pi}{T}\cdot T)-\frac{0}{2}+0 }=\frac{U}{\sqrt{T}}\sqrt{\frac{T}{2}-0-0+0}=\frac{U}{\sqrt{2}}}\)
Ostatecznie otrzymujemy \(\displaystyle{U_{RMS}=\frac{U}{\sqrt{2}}=\frac{2}{\sqrt{2}}=1,4\,\mathrm{V} }\)
Przebieg \(B\)
W tym przypadku wartość napięcia jest różna od zera w pierwszej połowie okresu. Obliczając wartość skuteczną wystarczy policzyć całkę z funkcji sinus w granicach od zera do \(\frac{T}{2}\). Całka w drugiej połowie okresu wyniesie zero.
\(\displaystyle{U_{RMS}=\sqrt{\frac{1}{T}\int_{0}^{0,5T} U^2\sin^2 (\omega t) \, dt} }\)
Przebieg obliczeń jest analogiczny jak w pierwszym przypadku.
\(\displaystyle{U_{RMS}=\sqrt{\frac{U^2}{T}\left [ \frac{t}{2}-\frac{1}{4\omega}\sin(2\omega t) \right ]^{0,5T}_0}}\)
\(\displaystyle{U_{RMS}=\frac{U}{\sqrt{T}}\sqrt{\frac{T}{4}-\frac{1}{4\omega}\sin(2\frac{2\pi}{T}\cdot \frac{T}{2})-\frac{0}{4}+0 }=\frac{U}{\sqrt{T}}\sqrt{\frac{T}{4}}=\frac{U}{2}}\)
Ostatecznie otrzymujemy \(\displaystyle{U_{RMS}=\frac{U}{2}=\frac{2}{2}=1\,\mathrm{V} }\)
Odpowiedź
Dla przebiegu \(A\) mamy \(\displaystyle{U_{RMS}=\frac{U}{\sqrt{2}}=1,4\,\mathrm{V} }\), natomiast dla \(B\) otrzymujemy \(\displaystyle{U_{RMS}=\frac{U}{2}=1\,\mathrm{V} }\).
