Zadanie 7.4.1.3
Wskazówka teoretyczna
Admitancja \(Y\) jest odwrotnością impedancji. Jednostką admitancji jest simens \(\displaystyle{\mathrm{S=\frac{1}{\Omega}}}\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Trochę więcej teorii
Impedancję opisuje funkcja zespolona, co oznacza, że w obliczeniach wykorzystujemy liczby zespolone. W opisie sygnałów sinusoidalnych jednostkę urojoną zapisujemy literką \(j\) - dla odróżnienia od prądów. Impedancja zastępcza układu jest zależna od częstotliwości i można ją opisać jako
\(\displaystyle{\overset{Z}{\_}(\omega)=Re\left \{ \overset{Z}{\_}\right \}+j\cdot Im\left \{ \overset{Z}{\_}\right \}\,\mathrm{[\Omega]} }\)
Impedancje zespolone elementów \(R,\, L,\, C\)
- dla idealnego rezystora: \(Z=R\)
- dla idealnej cewki indukcyjnej: \(\overset{Z}{\_}(\omega)=j X_L=j\cdot \omega L\), gdzie \(\omega\) to pulsacja \(\omega=2\pi f\), \(L\) - indukcyjność, \(X_L\) - reaktancja indukcyjna
- dla idealnego kondensatora: \(\displaystyle{\overset{Z}{\_}(\omega)=-j\cdot X_C=-j\frac{1}{\omega C}=\frac{1}{j\omega C} }\), gdzie \(C\) - pojemność, \(X_C\) - reaktancja pojemnościowa
\(\overset{Y}{\_}(\omega)=Re\left \{ \overset{Y}{\_}\right \}+j\cdot Im\left \{ \overset{Y}{\_}\right \}\,\mathrm{[S]}\)
Można admitancję zespoloną wyrazić w postaci wykładniczej
\(\displaystyle{\overset{Y}{\_}(\omega)=\frac{1}{Ze^{j\varphi }}=\frac{1}{Z}e^{-j\varphi }=Ye^{-j\varphi } }\)
Moduł admitancji zespolonej jest równy odwrotności modułu impedancji, a jej argument jest równy argumentowi impedancji zespolonej ze znakiem przeciwnym.
Admitancje zespolone elementów \(R,\, L,\, C\)
- dla idealnego rezystora: \(\displaystyle{Y=\frac{1}{R}=G}\), gdzie \(G\) - konduktancja
- dla idealnej cewki indukcyjnej: \(\displaystyle{\overset{Y}{\_}(\omega)=-j\cdot B_L=-j\frac{1}{\omega L}=\frac{1}{j\omega L}}\), gdzie \(\omega\) to pulsacja \(\omega=2\pi f\), \(L\) - indukcyjność, \(B_L\) - susceptancja indukcyjna \(\displaystyle{B_L=\frac{1}{X_L} }\)
- dla idealnego kondensatora: \(\displaystyle{\overset{Y}{\_}(\omega)=j\cdot B_C=j\omega C }\), gdzie \(C\) - pojemność, \(B_C\) - susceptancja pojemnościowa \(\displaystyle{B_C=\frac{1}{X_C} }\)
Analiza sytuacji
Dla wszystkich trzech układów mamy wyznaczyć impedancję, czyli opór zespolony. Wyznaczając wzory na impedancję zastępczą postępujemy tak samo jak przy obliczaniu rezystancji zastępczej, czyli opory dodajemy przy połączeniu szeregowym elementów. Przy połączeniu równoległym dodajemy odwrotności impedancji.
Rozwiązanie
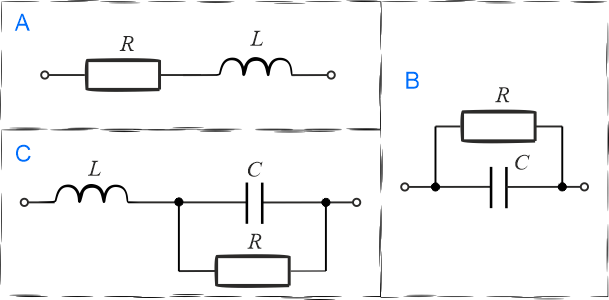
Schemat \(A\) - połączenie szeregowe induktora i rezystora
Impedancja zastępcza \(\overset{Z_A}{\_}\) to suma rezystancji i reaktancji zespolonej cewki indukcyjnej, czyli \(\overset{Z_A}{\_}=R+j\omega L\)
Admitancję można wyznaczyć jako
\(\displaystyle{\overset{Y_A}{\_}=\frac{1}{\overset{Z_A}{\_}}=\frac{1}{R+j\omega L} }\)
Ten sam wynik uzyskamy z formuły
\(\displaystyle{\overset{Y_A}{\_}=\frac{\frac{1}{R}\cdot\frac{1}{j\omega L}}{\frac{1}{R}+\frac{1}{j\omega L}}=\frac{1}{j\omega L R}\cdot\frac{j\omega L R}{j\omega L+R}=\frac{1}{R+j\omega L} }\)
Schemat \(B\) - połączenie równoległe kondensatora i rezystora
W tym przypadku łatwiej jest zacząć od admitancji zespolonej
\(\displaystyle{\overset{Y_B}{\_}=G+j\omega C }\)
Tą samą zależność uzyskamy dodając odwrotności impedancji
\(\displaystyle{\frac{1}{\overset{Z_B}{\_}}=\frac{1}{R}+\frac{1}{\frac{1}{j\omega C}}=G+j\omega C }\)
Impedancję zespoloną można wyznaczyć z zależności
\(\displaystyle{\overset{Z_B}{\_}=\frac{R\cdot\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}=\frac{R}{j\omega C}\cdot\frac{j\omega C}{j\omega CR+1}=\frac{R}{j\omega CR+1} }\)
Odwrotność impedancji jest tą samą zależnością co poprzednio
\(\displaystyle{\frac{1}{\overset{Z_B}{\_}}=\frac{j\omega CR+1}{R}=j\omega C+G }\)
Schemat \(C\) - połączenie mieszane induktora, kondensatora i rezystora
W tym przypadku mamy cewkę indukcyjną połączona szeregowo z równolegle połączonym rezystorem i kondensatorem. Impedancja zespolona zastępcza wyniesie więc
\(\displaystyle{\overset{Z_C}{\_}=j\omega L+\frac{R\cdot\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}=j\omega L+\frac{R}{j\omega CR+1}=\frac{j\omega L\left (j\omega CR+1\right )+R}{j\omega CR+1} }\)
Admitancja zespolona ma postać
\(\displaystyle{\overset{Y_C}{\_}=\frac{\left ( G+j\omega C \right )\cdot\frac{1}{j\omega L}}{\left ( G+j\omega C \right )+\frac{1}{j\omega L}} =\frac{j\omega CR+1}{j\omega LR}\cdot\frac{j\omega LR}{j\omega L+j\omega^2CLR+R}}\)
\(\displaystyle{\overset{Y_C}{\_}=\frac{j\omega CR+1}{j\omega L\left (j\omega CR+1\right )+R} }\)
Odpowiedź
Impedancje i admitancje zespolone dla kolejnych schematów wynoszą:
- \(\overset{Z_A}{\_}=R+j\omega L\) oraz \(\displaystyle{\overset{Y_A}{\_}=\frac{1}{R+j\omega L} }\)
- \(\displaystyle{\overset{Z_B}{\_}=\frac{R}{j\omega CR+1} }\) oraz \(\displaystyle{\overset{Y_B}{\_}=G+j\omega C }\)
- \(\displaystyle{\overset{Z_C}{\_}=\frac{j\omega L\left (j\omega CR+1\right )+R}{j\omega CR+1} }\) oraz \(\displaystyle{\overset{Y_C}{\_}=\frac{j\omega CR+1}{j\omega L\left (j\omega CR+1\right )+R} }\)
