Zadanie 7.4.1.5
Wskazówka teoretyczna
II prawo Kirchhoffa, dla rezystora i kondensatora połączonych szeregowo:
\(u_R(t)\) lub \(\displaystyle{\overset{U}{\_}_R}\) jest spadkiem napięcia na rezystorze, \(u_C(t)\), \(\displaystyle{\overset{U}{\_}_C}\) - napięcie na kondensatorze.
Natężenie prądu chwilowego na kondensatorze o pojemności \(C\)
W obwodzie z idealnym kondensatorem napięcie opóźnia się względem prądu o kąt fazowy \(\displaystyle{\varphi=-\frac{\pi}{2} }\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- kształt przebiegu napięcia \(U(t)=U_m\sin(\omega t)\).
Szukane:
- funkcja \(i(t)\) określająca wartości chwilowe prądu w układzie,
- wykresy czasowe i wskazowe.
Przebieg czasowy
Załóżmy, że do idealnego kondensatora podłączono źródło napięcia sinusoidalnego \(u_C(t)=U_m\sin(\omega t)\). Każdej zmianie napięcia towarzyszy zmiana ładunku na okładkach kondensatora. Stały prąd (ładowania) oznacza stałe tempo zmian napięcia na kondensatorze. Prąd jest wprost proporcjonalny nie do napięcia, jak dla opornika, lecz do szybkości zmian napięcia.
W obwodzie z idealnym kondensatorem napięcie opóźnia się względem prądu o kąt fazowy \(\displaystyle{\varphi=-\frac{\pi}{2} }\).
Z II prawa Kirchhoffa, dla rezystora i kondensatora połączonych szeregowo, przebieg czasowy napięcia wynosi
\(u_R(t)\) jest spadkiem napięcia na rezystorze, \(u_C(t)\) - napięcie na kondensatorze
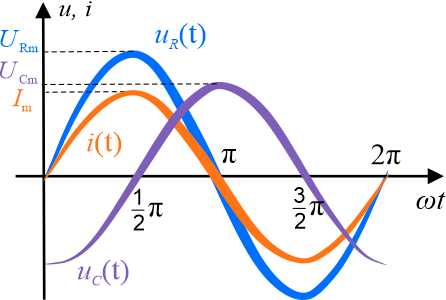
Na wykresie przedstawiono przebiegi dla \(i(t)=I_m\sin(\omega t)\) oraz \(\displaystyle{u(t)=u_R(t)+u_C(t)=RC\omega U_m\sin(\omega t) +U_m\sin(\omega t-\frac{\pi}{2}) }\)
Wykresy wskazowe
II prawo Kirchhoffa, dla rezystora i kondensatora połączonych szeregowo, w zapisie zespolonym ma postać
Rysowanie wykresu wskazowego rozpoczniemy od prądu płynącego w układzie. Wektor ten leży na osi \(Re\), ponieważ faza początkowa w podanym przebiegu czasowym wynosi zero \(i(t)=I_m\sin(\omega t+0)\). Z poprzedniego wykresu czasowego wnioskujemy, że prąd i napięcie na rezystorze są w fazie. Oznacza to, że nie występuje przesunięcie fazowe pomiędzy przebiegiem \(i(t)\) a \(u_R(t)\). Wektor reprezentujący napięcie na rezystorze również leży na osi poziomej (kąt \(\varphi = 0\) ).
W obwodzie z idealnym kondensatorem napięcie napięcie opóźnia się względem prądu o kąt fazowy \(\displaystyle{\varphi=-\frac{\pi}{2} }\), dlatego wektor reprezentujący napięcie na kondensatorze jest skierowany prostopadle w dół do wektora reprezentującego prąd.
Dodając graficznie dwa wektory \(U_R\) oraz \(U_C\) otrzymujemy wektor wypadkowy \(U\).
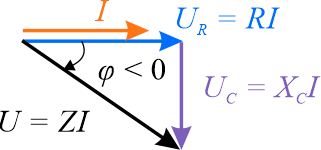
obliczeń na wartościach liczbowych.
Obliczenia
\(U_R = R\cdot I=100\cdot 0,25=25 \,\mathrm{V}\)
\(\displaystyle{X_C=\frac{1}{\omega C}=\frac{1}{2\cdot 3,14\cdot 1000\cdot 0,00001}=15,9\,\mathrm{\Omega} }\)
\(U_C=X_C\cdot I=15,9\cdot 0,25=3,98 \,\mathrm{V}\)
\(\displaystyle{\overset{U}{\_}=25\,e^{j\cdot 0}+3,98\,e^{-j\frac{\pi}{2}}=25-3,98j=25,3\,e^{-0,5608j}\,\mathrm{V} }\)
Obliczenia modułu wektora i kąt:
\(\displaystyle{\left | \overset{U}{\_} \right |=\sqrt{25^2+(3,98)^2}=25,3\,\mathrm{V} }\)
\(\displaystyle{\operatorname{tg}{\alpha}=\frac{U_C}{U_R}=\frac{-3,98}{25} }\), \(\displaystyle{\operatorname{arctg}{\alpha}=-0,5608\,\mathrm{rad} }\)
Zastosowania liczb zespolonych
Analizowany przebieg czasowy możemy przedstawić za pomocą wektora wirującego.
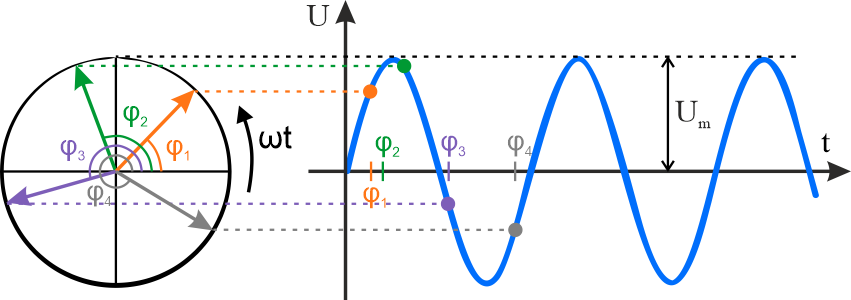
Narysujmy wektor wirujący w płaszczyźnie liczb zespolonych, którego rzuty na osie to odpowiednio \(a\) i \(b\).

Znając wartości \(a\) i \(b\) możemy obliczyć długość tego wektora \(\left | Z \right |=\sqrt{a^2+b^2}\). W ten sam sposób obliczamy moduł liczby zespolonej, która w zapisie algebraicznym ma postać \(Z=a+j\,b\). Odcinek skierowany od początku układu współrzędnych do punktu reprezentującego liczbę zespoloną nazywamy wskazem tej liczby.
Kąt nachylenia rozpatrywanego wektora obliczamy z definicji trygonometrycznych.
\(\displaystyle{\sin \varphi =\frac{b}{\left | Z \right |}}\) oraz \(\displaystyle{\cos \varphi =\frac{a}{\left | Z \right |}}\)
Po przekształceniu otrzymujemy:
\(b=\left | Z \right |\cdot \sin \varphi \) oraz \(a=\left | Z \right |\cdot \cos \varphi \)
Liczbę zespoloną można więc przedstawić jako \(Z=a+jb=\left | Z \right | \left ( \cos \varphi +j\sin \varphi \right )\)
Przedstawienie symboliczne przebiegów sinusoidalnych
Niech przebieg czasowy będzie opisany funkcją \(i(t)=I_m\sin (\omega t+\varphi)\). W zapisie zespolonym taki przebieg można zapisać w następujący sposób:
Wyrażenie \(\displaystyle{\overset{I}{\_}=\frac{I_m}{\sqrt 2}\, e^{j\varphi}}\) nosi nazwę zespolonej wartości skutecznej przebiegu sinusoidalnego.
Jednoznaczne reprezentowanie symboliczne przebiegu sinusoidalnego wymaga podania zespolonej wartości skutecznej oraz częstotliwości (lub pulsacji) sygnału.
Przykład
Natężenie prądu sinusoidalnego wynosi \(\displaystyle{i(t)=0,1\sin\left (314 t+ \frac{\pi}{3} \right )\,\mathrm{A} }\). Zapisz wartość zespoloną skuteczną prądu.
\(\displaystyle{\overset{I}{\_}=\frac{I_m}{\sqrt 2}\, e^{j\varphi}=\frac{0,1}{\sqrt 2}\,e^{j\frac{\pi}{3}}\,\mathrm{A} }\), \(\omega=314=2\pi f=2\cdot 3,14\cdot 50\), częstotliwość \(f=50\,\mathrm{Hz}\)
Wykresy przedstawiające zespolone wartości skuteczne nazywamy wykresami wskazowymi.

