Zadanie 7.4.2.1
  1. Kurs obliczeniowy z fizyki
  2. 7. Elektryczność
  3. 7.4. Obwody prądu przemiennego i tętniącego
  4. 7.4.2. Trening
  5. Zadanie 7.4.2.1

 Zadanie 7.4.2.1

Wartość średnia i międzyszczytowa
Zmierzono trzy różne przebiegi napięcia. Wyznacz wartość międzyszczytową oraz średnią dla tych przebiegów. Wartość napięcia \(U\) na każdym z wykresów wynosi \(2\,\mathrm{V}\). Wykresy \(A\) i \(B\) różnią się współczynnikiem wypełnienia.
Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
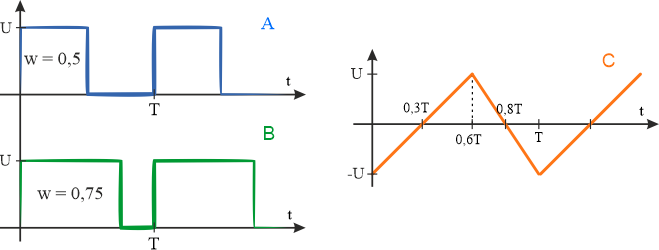
- Przebiegi czasowe napięcia,
- napięcia zaznaczone na każdym z wykresów wynosi \(U=2\,\mathrm{V}\),
- współczynnik wypełnienia dla sygnału \(A\): \(w_a=0,5\),
- współczynnik wypełnienia dla sygnału \(B\): \(w_b=0,75\).

Szukane:
- wartość międzyszczytowa dla trzech przebiegów napięć: \(Ua_{p-p}\), \(Ub_{p-p}\), \(Uc_{p-p}\).
- wartość średnia dla trzech przebiegów napięć: \(Ua_{AV}\), \(Ub_{AV}\), \(Uc_{AV}\).

Odpowiedź

Dla kolejnych przebiegów mamy:

  • \(A\): \(U_{p-p}=2\,\mathrm{V}\) oraz \(U_{AV}=1\,\mathrm{V}\)
  • \(B\): \(U_{p-p}=2\,\mathrm{V}\) oraz \(U_{AV}=1,5\,\mathrm{V}\)
  • \(C\): \(U_{p-p}=4\,\mathrm{V}\) oraz \(U_{AV}=0\,\mathrm{V}\)

Polecenie

Wyznacz wartość międzyszczytową oraz średnią dla przebiegu \(A\). Wybierz jeden prawidłowy zestaw wartość spośród czterech.

Wybór 1 z 4

\(U_{p-p}=1\,\mathrm{V}\)
\(U_{AV}=1\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(U_{p-p}=2\,\mathrm{V}\)
\(U_{AV}=2\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(U_{p-p}=1\,\mathrm{V}\)
\(U_{AV}=2\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(U_{p-p}=2\,\mathrm{V}\)
\(U_{AV}=1\,\mathrm{V}\)

Odpowiedź prawidłowa

Rozwiązanie

Wartość napięcia zmienia się od wartości minimalnej \(0\) do maksymalnej \(2\,\mathrm{V}\). Napięcie międzyszczytowe wynosi więc \(U_{p-p}=2\,\mathrm{V}\).

Wartość średnią napięcia wyznaczamy ze wzoru \(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{\tau}u(t)\, dt}\) gdzie \(\tau\) jest czasem, w którym napięcie przyjmuje wartość \(U\).

\(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{\tau}U\, dt =\frac{1}{T}\cdot U\cdot \left [ t \right ]^{\tau}_0=\frac{\tau}{T}\cdot U }\)

Wyrażenie \(\displaystyle{\frac{\tau}{T}=w }\) jest równe współczynnikowi wypełnienia. Wartość średnią napięcia wynosi

\(U_{AV}=w_a\cdot U=0,5\cdot 2=1\,\mathrm{V}\)

Polecenie

Wyznacz wartość międzyszczytową oraz średnią dla przebiegu \(B\). Wybierz jeden prawidłowy zestaw wartość spośród czterech.

Wybór 1 z 4

\(U_{p-p}=1,5\,\mathrm{V}\)
\(U_{AV}=1,5\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(U_{p-p}=1,5\,\mathrm{V}\)
\(U_{AV}=2\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(U_{p-p}=2\,\mathrm{V}\)
\(U_{AV}=1,5\,\mathrm{V}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(U_{p-p}=2\,\mathrm{V}\)
\(U_{AV}=2\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Wartość napięcia zmienia się od wartości minimalnej \(0\) do maksymalnej \(2\,\mathrm{V}\). Napięcie międzyszczytowe wynosi więc \(U_{p-p}=2\,\mathrm{V}\).

Wartość średnią napięcia, jak poprzednio, wyznaczamy ze wzoru \(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{\tau}u(t)\, dt}\) gdzie \(\tau\) jest czasem, w którym napięcie przyjmuje wartość \(U\).

\(\displaystyle{U_{AV}=\frac{1}{T}\int_{0}^{\tau}U\, dt =w_b\cdot U }\)
 
\(U_{AV}=w_a\cdot U=0,75\cdot 2=1,5\,\mathrm{V}\)

Polecenie

Wyznacz wartość międzyszczytową oraz średnią dla przebiegu \(C\). Wybierz jeden prawidłowy zestaw wartość spośród czterech.

Wybór 1 z 4

\(U_{p-p}=2\,\mathrm{V}\)
\(U_{AV}=0\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(U_{p-p}=4\,\mathrm{V}\)
\(U_{AV}=0\,\mathrm{V}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(U_{p-p}=4\,\mathrm{V}\)
\(U_{AV}=1\,\mathrm{V}\)

Odpowiedź nieprawidłowa

wybór 4 z 4

\(U_{p-p}=4\,\mathrm{V}\)
\(U_{AV}=2\,\mathrm{V}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Wartość międzyszczytowa wynosi \(2U=4\,\mathrm{V}\).

Na podstawie wykresu możemy zbocze rosnące i malejące przedstawić za pomocą dwóch funkcji.

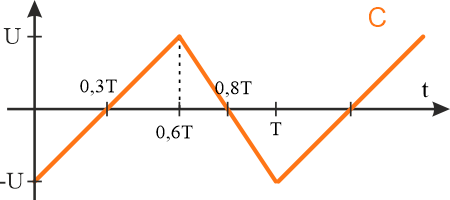
Rysunek


Równanie pierwszej prostej można wyznaczyć z punktów, np. \(\left ( 0,3T;\, 0 \right )\) oraz \(\left ( 0,6T;\, U \right )\). Funkcja liniowa przechodząca przez te dwa punkty ma postać

\(\displaystyle{u_1(t)=\frac{10}{3}\frac{U}{T}\cdot t-U  }\)

Druga prosta przechodzi przez punkty \(\left ( 0,8T;\, 0 \right )\) oraz \(\left ( T;\, -U \right )\) i ma postać

\(\displaystyle{u_2(t)=-5\frac{U}{T}\cdot t +4U  }\)

Wartość średnia wynosi:

\(\displaystyle{U_{AV}=\frac{1}{T}\left ( \int_{0}^{0,6T}\left ( \frac{10}{3}\frac{U}{T}\cdot t-U \right )dt+\int_{0,6T}^{T} \left ( -5\frac{U}{T}\cdot t +4U \right )dt\right )  }\)

\(\displaystyle{U_{AV}=\frac{1}{T}\frac{10}{6}\frac{U}{T}\left [ t^2 \right ]^{0,6T}_0-\frac{1}{T}U\left [ t \right ]^{0,6T}_0-\frac{1}{T}\frac{5}{2}\frac{U}{T}\left [ t^2 \right ]^{T}_{0,6T}+4\frac{U}{T}\left [ t \right ]^{T}_{0,6T}  }\)

\(\displaystyle{U_{AV}=\frac{6}{10}U-\frac{6}{10}U-\frac{5}{2}U+\frac{9}{10}U+4U-\frac{12}{5}U=0 }\)

Odpowiedź

Dla kolejnych przebiegów mamy:

  • \(A\): \(U_{p-p}=2\,\mathrm{V}\) oraz \(U_{AV}=1\,\mathrm{V}\)
  • \(B\): \(U_{p-p}=2\,\mathrm{V}\) oraz \(U_{AV}=1,5\,\mathrm{V}\)
  • \(C\): \(U_{p-p}=4\,\mathrm{V}\) oraz \(U_{AV}=0\,\mathrm{V}\)