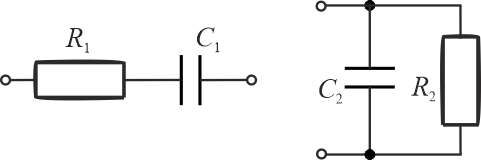
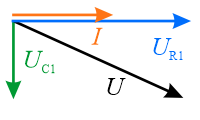Zadanie 7.4.2.5
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 7. Elektryczność
  3. 7.4. Obwody prądu przemiennego i tętniącego
  4. 7.4.2. Trening
  5. Zadanie 7.4.2.5

 Zadanie 7.4.2.5

Rzeczywisty kondensator
Na rysunku przedstawiono schematy zastępcze rzeczywistego kondensatora szeregowy i równoległy. Mając dane \(C_2=100\,\mathrm{nF}\) i \(R_2=2,5\,\mathrm{k\Omega}\) wyznacz \(R_1\) oraz \(C_1\), dla których oba schematy są równoważne. Narysuj wykresy wskazowe dla tych układów. Napięci na zaciskach jest sinusoidalne, a jego faza początkowa jest równa zeru. Częstotliwość wynosi \(f=500\,\mathrm{Hz}\).
Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- pojemność kondensatora \(C_2=100\,\mathrm{nF}\),
- rezystancja \(R_2=2,5\,\mathrm{k\Omega}\),
- częstotliwość \(f=500\,\mathrm{Hz}\).

Szukane:
- pojemność kondensatora \(C_1\),
- rezystancja \(R_1\).

Odpowiedź

Szukana rezystancja i pojemność wynoszą \(R_1=1546\,\mathrm{\Omega}\)  oraz  \(C_1=262\,\mathrm{nF}\). Wykresy wskazowe dla układu pierwszego i drugiego:

  

Polecenie

Oblicz rezystancję rezystora \(R_1\) oraz pojemność kondensatora \(C_1\) Wybierz jeden prawidłowy zestaw wartość z dwóch możliwych.

Wybór 1 z 2

\(R_1=1546\,\mathrm{\Omega}\)
\(C_1=262\,\mathrm{nF}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(R_1=154,7\,\mathrm{\Omega}\)
\(C_1=2,62\,\mathrm{nF}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Impedancje zastępcze dla układów wynoszą

\(\displaystyle{\overset{Z}{\_}_1=R_1-j\,\frac{1}{\omega C_1} }\)  
\(\displaystyle{\overset{Y}{\_}_2=G_2+j\omega C_2}\) i stąd  \(\displaystyle{\overset{Z}{\_}_2=\frac{ 1 }{G_2+j\omega C_2} }\)  gdzie  \(\displaystyle{G_2=\frac{1}{R_2} }\)

Dla określonej częstotliwości obydwa układy są równoważne, gdy równe są ich impedancje (admitancje) zespolone. Należy teraz zapisać tak impedancje zastępcze, aby można było porównać części rzeczywiste i części urojone.

\(\displaystyle{\overset{Z}{\_}_2=\frac{G_2-j\omega C_2}{G_2^2+\omega^2C_2^2}=\frac{G_2}{G_2^2+\omega^2C_2^2}-j\,\frac{\omega C_2}{G_2^2+\omega^2C_2^2} }\)

\(\displaystyle{R_1=\frac{G_2}{G_2^2+\omega^2C_2^2}=1546\,\mathrm{\Omega} }\) 
 
\(\displaystyle{\frac{1}{\omega C_1}=\frac{\omega C_2}{G_2^2+\omega^2C_2^2} }\)  i stąd  \(\displaystyle{C_1=\frac{ G_2^2+\omega^2C_2^2}{\omega^2 C_2}=262\,\mathrm{nF}}\)

Polecenie

Narysuj wykres wskazowy dla układu z elementami \(R_1\) i \(C_1\). Wybierz jeden prawidłowy wykres z dwóch możliwych.

Wybór 1 z 2

Odpowiedź prawidłowa

Wybór 2 z 2

Odpowiedź nieprawidłowa

Rozwiązanie

Jeżeli do zacisków dwójnika przyłożymy napięcie, to w obwodzie popłynie prąd, który spowoduje powstanie napięć na elementach układu. Z II prawa Kirchhoffa mamy

\(\displaystyle{\overset{U}{\_}=\overset{U}{\_}_{R1}+\overset{U}{\_}_{C1}=\left ( R_1-j\,\frac{1}{\omega C_1} \right )\overset{I}{\_}=\overset{Z}{\_}_1\cdot \overset{I}{\_} }\). 

Napięcie na kondensatorze opóźnia się w fazie względem prąd o kąt \(\varphi\), którego tangens obliczymy jako argument impedancji układu

\(\displaystyle{\operatorname{tg}{\varphi}=-\frac{\frac{1}{\omega C_1}}{R_1}=-\frac{1}{\omega C_1R_1}=-0,78585 }\)
\(\displaystyle{\varphi=\operatorname{arctg}{(-0,78585)} =-0,6661\,\mathrm{rad}  }\)

Wektor reprezentujący napięcie na induktorze jest prostopadły do wektora reprezentującego prąd i skierowany w dół. Kąt \(\varphi\) jest ujemny. Jest to kąt nachylenia wektora reprezentującego napięcie \(U\).

Polecenie

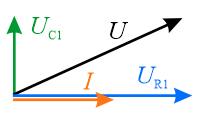
Narysuj wykres wskazowy dla układu z elementami \(R_2\) i \(C_2\). Wybierz jeden prawidłowy wykres z dwóch możliwych.

Wybór 1 z 2

Odpowiedź prawidłowa

Wybór 2 z 2

Odpowiedź nieprawidłowa

Rozwiązanie

Z I prawa Kirchhoffa mamy

\(\displaystyle{\overset{I}{\_}=\overset{I}{\_}_{R2}+\overset{I}{\_}_{C2}=\left ( G_2-j\frac{1}{\omega C_2} \right )\overset{U}{\_}=\overset{Y}{\_}_2\cdot \overset{U}{\_} }\). 

Prąd ten wyprzedza napięcia o kąt fazowy \(\varphi\), którego tangens obliczamy jako argument admitancji

\(\displaystyle{\operatorname{tg}{\varphi}=\frac{\omega C_2}{G_2}=0,7854 }\)
\(\displaystyle{\varphi=\operatorname{arctg}{(0,7854)}=0,6655\,\mathrm{rad} }\)

Wektor reprezentujący prąd na kondensatorze jest prostopadły do wektora reprezentującego napięcie i skierowany do góry. Kąt \(\varphi\) jest to kąt nachylenia wektora reprezentującego prąd \(I\).

Odpowiedź

Szukana rezystancja i indukcyjność wynoszą \(R_1=1546\,\mathrm{\Omega}\)  oraz  \(C_1=262\,\mathrm{nF}\). Wykresy wskazowe dla układu pierwszego i drugiego: