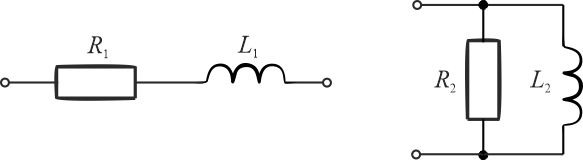
Zadanie 7.4.2.4
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 7. Elektryczność
  3. 7.4. Obwody prądu przemiennego i tętniącego
  4. 7.4.2. Trening
  5. Zadanie 7.4.2.4

 Zadanie 7.4.2.4

Rzeczywisty induktor
Na rysunku przedstawiono schematy zastępcze rzeczywistej cewki indukcyjnej szeregowy i równoległy. Mając dane \(L_2=2\,\mathrm{H}\) i \(R_2=40\,\mathrm{\Omega}\) wyznacz \(R_1\) oraz \(L_1\), dla których oba schematy są równoważne. Narysuj wykresy wskazowe dla tych układów. Do zacisków układu przyłożono napięcie sinusoidalne. Częstotliwość wynosi \(f=20\,\mathrm{Hz}\).
Rysunek

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- indukcyjność cewki \(L_2=2\,\mathrm{H}\),
- rezystancja \(R_2=40\,\mathrm{\Omega}\),
- częstotliwość \(f=20\,\mathrm{Hz}\).

Szukane:
- indukcyjność cewki \(L_1\),
- rezystancja \(R_1\).

Odpowiedź

Szukana rezystancja i indukcyjność wynoszą \(R_1=39\,\mathrm{\Omega}\)  oraz  \(L_1=49,4\,\mathrm{mH}\). Wykresy wskazowe dla układu pierwszego i drugiego:

  

Polecenie

Oblicz rezystancję rezystora \(R_1\) oraz indukcyjność cewki \(L_1\) Wybierz jeden prawidłowy zestaw wartość z dwóch możliwych.

Wybór 1 z 2

\(R_1=39\,\mathrm{\Omega}\)
\(L_1=49,4\,\mathrm{mH}\)

Odpowiedź prawidłowa

Wybór 2 z 2

\(R_1=390\,\mathrm{\Omega}\)
\(L_1=49\,\mathrm{H}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Impedancje zastępcze dla układów wynoszą

\(\displaystyle{\overset{Z}{\_}_1=R_1+j\omega L_1 }\)  oraz  \(\displaystyle{\overset{Z}{\_}_2=\frac{ j\omega L_2\cdot R_2 }{j\omega L_2+R_2} }\)

Dla określonej częstotliwości obydwa układy są równoważne, gdy równe są ich impedancje (admitancje) zespolone. Należy teraz zapisać tak impedancje zastępcze, aby można było porównać części rzeczywiste i części urojone.

\(\displaystyle{\overset{Z}{\_}_2=\frac{R_2\cdot j\omega L_2\left ( R_2 -j\omega L_2\right )}{\left ( R_2 +j\omega L_2\right )\left ( R_2 -j\omega L_2\right )}=\frac{j\,R_2^2\omega L_2+\omega^2L_2^2R_2}{R_2^2+\omega^2L_2^2} }\)

\(\displaystyle{R_1=\frac{\omega^2L_2^2R_2}{R_2^2+\omega^2L_2^2}=39\,\mathrm{\Omega} }\)  oraz  \(\displaystyle{\omega L_1=\frac{\omega L_2R_2^2}{R_2^2+\omega^2L_2^2}}\)

\(\displaystyle{L_1=\frac{ L_2R_2^2}{R_2^2+\omega^2L_2^2}=49,4\,\mathrm{mH}}\)

Polecenie

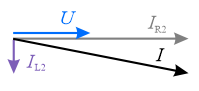
Narysuj wykres wskazowy dla układu z elementami \(R_1\) i \(L_1\). Wybierz jeden prawidłowy wykres z dwóch możliwych.

Wybór 1 z 2

Odpowiedź prawidłowa

Wybór 2 z 2

Odpowiedź nieprawidłowa

Rozwiązanie

Z II prawa Kirchhoffa mamy

\(\displaystyle{\overset{U}{\_}=\overset{U}{\_}_{R1}+\overset{U}{\_}_{L1}=\left ( R_1+j\omega L_1 \right )\overset{I}{\_}=\overset{Z}{\_}_1\cdot \overset{I}{\_} }\). 

Napięcie na induktorze wyprzedza w fazie prąd, którego tangens wynosi

\(\displaystyle{\operatorname{tg}{\varphi}=\frac{\omega L_1}{R_1}=0,1605\,\mathrm{rad} }\)

Wektor reprezentujący napięcie na induktorze jest prostopadły do wektora reprezentującego prąd i skierowany do góry. Kąt \(\varphi\) jest dodatni. Jest to kąt nachylenia wektora reprezentującego napięcie \(U\).

Polecenie

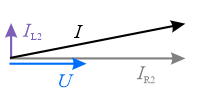
Narysuj wykres wskazowy dla układu z elementami \(R_2\) i \(L_2\). Wybierz jeden prawidłowy wykres z dwóch możliwych.

Wybór 1 z 2

Odpowiedź prawidłowa

Wybór 2 z 2

Odpowiedź nieprawidłowa

Rozwiązanie

Z I prawa Kirchhoffa mamy

\(\displaystyle{\overset{I}{\_}=\overset{I}{\_}_{R2}+\overset{I}{\_}_{L2}=\left ( G_2-j\frac{1}{\omega L_2} \right )\overset{U}{\_}=\overset{Y}{\_}_2\cdot \overset{U}{\_} }\). 

Prąd ten opóźnia się w fazie względem napięcia o kąt \(\varphi\), którego tangens obliczamy jako argument admitancji

\(\displaystyle{\operatorname{tg}{\varphi}=\frac{R_2}{\omega L_2}=0,1578\,\mathrm{rad} }\)

Wektor reprezentujący pąd na induktorze jest prostopadły do wektora reprezentującego napięcie i skierowany w dół. Kąt \(\varphi\) jest ujemny. Z obliczeń wyszła wartość dodatnia, ponieważ argument admitancji ma znak przeciwny do argumentu impedancji. Jest to kąt nachylenia wektora reprezentującego prąd \(I\).

Odpowiedź

Szukana rezystancja i indukcyjność wynoszą \(R_1=39\,\mathrm{\Omega}\)  oraz  \(L_1=49,4\,\mathrm{mH}\). Wykresy wskazowe dla układu pierwszego i drugiego: