Zadanie 7.4.2.3
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
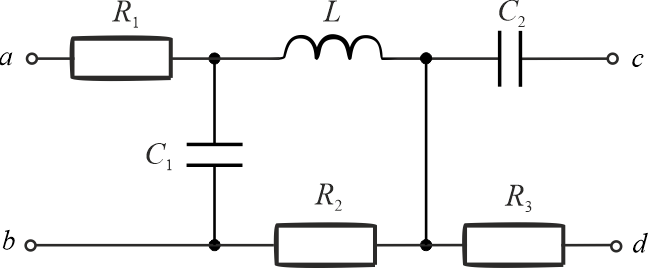
- elementy przedstawione na schemacie \(R_1\), \(R_2\), \(R_3\), \(L\), \(C_1\), \(C_2\).
Szukane:
- impedancja zastępcza \(\overset{Z_{ab}}{\_} \) oraz \(\overset{Z_{cd}}{\_} \).
Odpowiedź
Impedancje zastępcze wynoszą: \(\displaystyle{\overset{Z}{\_}_{ab}=\frac{j\omega L+ R_2}{j\omega C_1 \left ( j\omega L+ R_2 \right )+1}+R_1}\) oraz \(\displaystyle{\overset{Z}{\_}_{cd}=R_3-\frac{j}{\omega C_2} }\).
Polecenie
Wyznacz impedancję zastępczą \(\large{\overset{Z_{ab}}{\_}} \). Wybierz jedno prawidłowe równanie z dwóch możliwych.
\(\displaystyle{\overset{Z}{\_}_{ab}=\frac{j\omega L+ R_2}{j\omega C_1 \left ( j\omega L+ R_2 \right )+1}+R_1}\)
\(\displaystyle{\overset{Z}{\_}_{ab}=\frac{j\omega L+ R_2}{j\omega C_1 \left ( j\omega L+ R_2 \right )+1}+R_1+R_3+\frac{1}{j\omega C_2}}\)
Rozwiązanie
W tym przypadku zaciski \(cd\) są rozwarte, więc prąd nie płynie przez elementy \(C_2\) i \(R_3\). Elementy \(L\) oraz \(R_2\) są połączone szeregowo i razem tworzą połączenie równoległe z \(C_1\). Impedancję można zapisać jako
\(\displaystyle{\overset{Z}{\_}_{ab}=\frac{\left ( j\omega L+R_2 \right )\frac{1}{j\omega C_1}}{j\omega L+R_2 +\frac{1}{j\omega C_1}}+R_1=\frac{j\omega L+ R_2}{j\omega C_1 \left ( j\omega L+ R_2 \right )+1}+R_1}\)
Polecenie
Wyznacz impedancję zastępczą \(\large{\overset{Z_{cd}}{\_}} \). Wybierz jedno prawidłowe równanie z dwóch możliwych.
}\)
Rozwiązanie
Patrząc na układ od strony zacisków \(cd\) widzimy, że za kondensatorem \(C_2\) oraz rezystorem \(R_3\) jest zwarcie, zatem w obwodzie mamy tylko te dwa elementy. Można na tą sytuację jeszcze popatrzeć w inny sposób. Elementy \(L\), \(C_1\) i \(R_2\) są połączone szeregowo. Zapiszmy ich impedancję jako \(\displaystyle{\overset{Z}{\_}_1=R_2+j\omega L-\frac{j}{\omega C_1} }\). Zamiast pionowego przewodu wyobraźmy sobie opornik o rezystancji zero. Rezystor ten jest podłączony równolegle do impedancji \(\overset{Z}{\_}_1\), zatem \(\displaystyle{\overset{Z}{\_}_{10}=\frac{\overset{Z}{\_}_1\cdot 0}{\overset{Z}{\_}_1+0}=0}\).
Impedancja zastępcza układu tym razem wynosi \(\displaystyle{\overset{Z}{\_}_{cd}=R_3-\frac{j}{\omega C_2} }\)
Odpowiedź
Impedancje zastępcze wynoszą: \(\displaystyle{\overset{Z}{\_}_{ab}=\frac{j\omega L+ R_2}{j\omega C_1 \left ( j\omega L+ R_2 \right )+1}+R_1}\) oraz \(\displaystyle{\overset{Z}{\_}_{cd}=R_3-\frac{j}{\omega C_2} }\).
