Wektor \(\vec{a}\) tworzy z osią \(x\) kartezjańskiego układu współrzędnych kąt równy \(240^{\circ}\). Należy przedstawić ten wektor w postaci: \(\vec{a}=x\hat{i}+y\hat{j}\), gdzie \(\hat{i}\), \(\hat{j}\) są wektorami jednostkowymi odpowiednich osi (wersorami). Długość wektora \(\vec{a}\) wynosi \(2\).
Wskazówka teoretyczna
Teoria - kąt w układzie współrzędnych
Jak narysować kąt w układzie współrzędnych?
Dane i szukane
Dane: - długość wektora \(\vec{a}\): \(a=2\), - miara kąta pomiędzy osią x kartezjańskiego układu współrzędnych a wektorem \(\vec{a}\): \(\alpha =240^{\circ}\).
Szukane: - współrzędne wektora \(\vec{a}\).
Zapisanie wektora z wykorzystaniem wersorów: \(\vec{a}=x\hat{i}+y\hat{j}\), jest równoważne przedstawieniu go w postaci sumy dwu wektorów: jednego wzdłuż osi OX, a drugiego wzdłuż osi OY. Należy zatem naszkicować położenie tego wektora w kartezjańskim układzie współrzędnych i rozłożyć go graficznie na wektory składowe, wzdłuż odpowiednich osi.
Rysunek. a) Wektor \(\vec{a}\) przedstawiony w układzie kartezjańskim: \(a_{x}\) oraz \(a_{y}\) oznaczają dwie składowe wektora \(\vec{a}\), kolorem czarnym zostały narysowane wersory. b) rysunek pomocniczy – zapis funkcji cosinus oraz sinus.
Rysunek. a) Wektor \(\vec{a}\) przedstawiony w układzie kartezjańskim: \(a_{x}\) oraz \(a_{y}\) oznaczają dwie składowe wektora \(\vec{a}\), kolorem czarnym zostały narysowane wersory. b) rysunek pomocniczy – zapis funkcji cosinus oraz sinus.
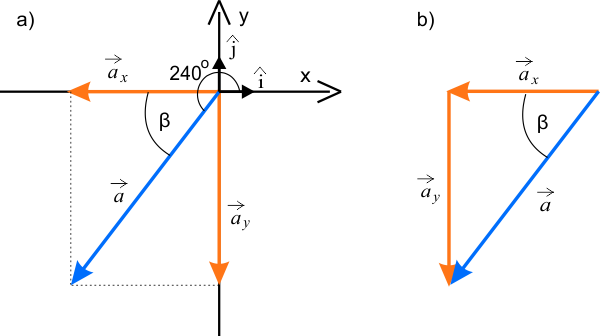
Rozwiązanie
Na powyższym rysunku został wprowadzony pomocniczy kąt \(\beta=240^{\circ}-180^{\circ}\). Kąt \(\beta\) można użyć do obliczenia składowych wektora \(a_{x}\) oraz \(a_{y}\).
Zgodnie z danymi zadania długość wektora wynosi \(2\) \((a=2)\). Składową \(a_{x}\) można policzyć korzystając z definicji funkcji trygonometrycznych:
\(\displaystyle{\cos\beta=\frac{a_{x}}{a}}\) mnożąc stronami przez a otrzymujemy:
Wartość wektora \(\vec{a_{x}}\) jest ujemna, ponieważ skierowany jest on przeciwnie do wersora \(\hat{i}\), więc \(a_{x}=-1\) Analogicznie postępujemy dla składowej \(a_{y}\)
