Zadanie 1.2.2.3
  1. Kurs obliczeniowy z fizyki
  2. 1. Wektory
  3. 1.2 Wektory w układzie kartezjańskim
  4. 1.2.2 Trening
  5. Zadanie 1.2.2.3

 Zadanie 1.2.2.3

Rzuty wektora na osie
Wektor \(\vec{a}\) tworzy z osią \(OX\) kartezjańskiego układu współrzędnych kąt równy \(135^{\circ}\). Przedstaw ten wektor w postaci: \(\displaystyle{\vec{a}=(-3\hat{i}+y\hat{j})\;\mathrm{\frac{m}{s^2}}}\), gdzie \(\hat{i}\), \(\hat{j}\) są wektorami jednostkowymi odpowiednich osi. Oblicz \(y\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Odpowiedź

Współrzędne wektora \(\vec{a}\) wynoszą \(\displaystyle{\vec{a}=-3\hat{i}+3\hat{j}\;\mathrm{\left [\frac{m}{s^2}\right ]}}\).

Polecenie

Wybierz z dwóch zestawów, dane pasujące do treści zadania. Prawidłowa odpowiedź odsłoni dalszą część zadania.

Dane:
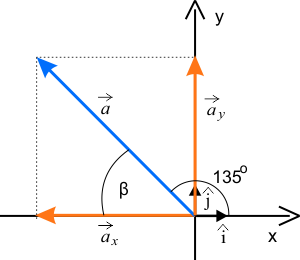
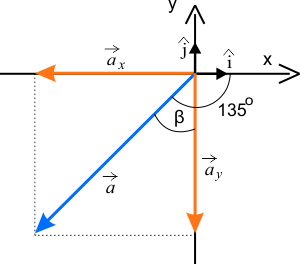
- współrzędna x-owa wektora \(\vec{a}\) wynosi: \(a_{x}=-3\),
- miara kąta pomiędzy osią x kartezjańskiego układu współrzędnych a wektorem \(\vec{a}\): \(\alpha =135^{\circ}\).

Szukane:
- współrzędne wektora \(\vec{a}\).

Odpowiedź prawidłowa

Dane:
-długość wektora \(\vec{a}\): \(a=3\),
- miara kąta pomiędzy osią \(OX\) kartezjańskiego układu współrzędnych a wektorem \(\vec{a}\): \(\alpha =135^{\circ}\).

Szukane:
- współrzędne wektora \(\vec{a}\).

Odpowiedź nieprawidłowa.
W zadaniu nie było podanej długości wektora \(\vec{a}\).

Pytanie

Który rysunek jest prawidłowy? Wybierz jeden spośród dwóch. Prawidłowa odpowiedź odsłoni dalszą część rozwiązania.

Wektor \(\vec{a}\) przedstawiony w układzie kartezjańskim

Odpowiedź prawidłowa

Wektor \(\vec{a}\) przedstawiony w układzie kartezjańskim

Odpowiedź nieprawidłowa
Nieprawidłowo zostal zaznaczony kąt \(\alpha =135^{\circ}\).
Na powyższym rysunku został wprowadzony pomocniczy kąt \(\beta=180^{\circ}-135^{\circ}=45^{\circ}\). Kąt \(\beta\) można użyć do obliczenia składowych wektora \(a_{y}\).

Polecenie

Wskaż, wśród 4 wartości, liczbę określająca współrzędną \(y\) wektora \(\vec{a}\).

Wybór 1 z 4

\(y=-3\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(y=1\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(y=3\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(y=-1\)

Odpowiedź nieprawidlowa

Rozwiązanie

Obliczenia przeprowadzane sa dla trójkąta prostokątnego o jednej przyprostokątnej długości \(3\) i kąta \(\beta=45^{\circ}\).

\(\displaystyle{ tg(\beta)=\frac{a_x}{a_{y}}}\)
\(\displaystyle{ tg(\beta)=\frac{3}{a_{y}}}\)
\(\displaystyle{ a_{y}=\frac{3}{tg(45^{\circ})}=\frac{3}{1}=3\;\mathrm{\frac{m}{s^2}}}\)

Odpowiedź

Współrzędne wektora \(\vec{a}\) wynoszą \(\displaystyle{\vec{a}=-3\hat{i}+3\hat{j}\;\mathrm{\left [\frac{m}{s^2}\right ]}}\).