Zadanie 1.3.2.5
Zadanie
Dwa wektory zręcznie położone na składowe są rozłożone. Wektor \(\vec{b}=3\,\hat{i}+4\,\hat{j}\) na \(\vec{a}=6\,\hat{i}+3\,\hat{j}\) jest rzucony. Pamiętaj, że nie na osie rzut tylko jest dozwolony. Wyznacz składowe wektora \(\vec{b}\) w odniesieniu do wektora \(\vec{a}\). Dane są dwa wektory \(\vec{a}=6\,\hat{i}+3\,\hat{j}\) oraz \(\vec{b}=3\,\hat{i}+4\,\hat{j}\). Rozłóż wektor \(\vec{b}\) na składową równoległą do wektora \(\vec{a}\) oraz do niego prostopadłą.
Informacja
Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- wektor pierwszy o współrzędnych \(\vec{a}=6\,\hat{i}+3\,\hat{j}\),
- wektor drugi o współrzędnych \(\vec{b}=3\,\hat{i}+4\,\hat{j}\).
Szukane:
- Składowe wektora \(\vec{b}\) wyznaczone względem wektora \(\vec{a}\).
Odpowiedź
Składowe wektora \(\vec{b}\) wyznaczone względem wektora \(\vec{a}\) wynoszą \(\vec{b_{1}}=4\,\hat{i}+2\,\hat{j}\) oraz \(\vec{b_{2}}=-\hat{i}+2\,\hat{j}\).
Polecenie
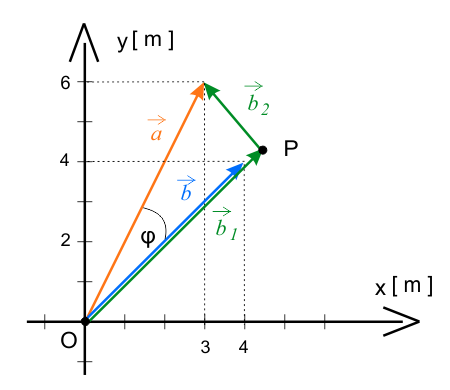
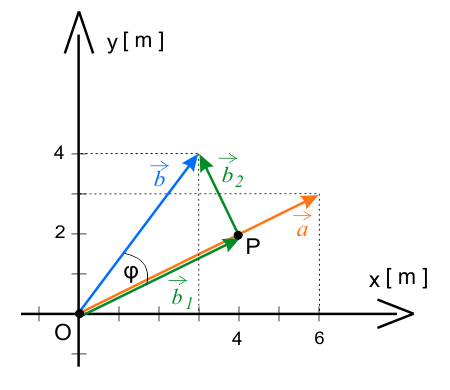
Wybierz, spośród dwóch, rysunek, który ilustruje treść zadania.
Polecenie
Korzystając z własności trójkąta prostokątnego wyznacz długość odcinka \(OP\) (długość wektora \(\vec{b_{1}}\)). Wybierz, spośród trzech, jedną prawidłowa odpowiedź.
\(\displaystyle{\cos\,\varphi=\frac{b_{1}}{b}}\) oraz \(\displaystyle{\cos\,\varphi=\frac{\vec{a}\circ \vec{b}}{a\cdot b}}\)
Rozwiązanie - etap 1
Iloczyn skalarny wynosi:
\(\vec{a}\circ \vec{b}=x_{a}\cdot x_{b}+y_{a}\cdot y_{b}+z_{a}\cdot z_{b}\)
\(\vec{a}\circ \vec{b}=6\cdot 3+3\cdot 4=30\)
Długość wektora \(\vec{a}\): \(a=\sqrt{6^{2}+3^{2}}=\sqrt{45}=3\sqrt{5}\)
\(\displaystyle{\left|OP\right|=b_{1}=b\cdot \cos\,\varphi=b\cdot \frac{\vec{a}\circ \vec{b}}{a\cdot b}}\)
\(\displaystyle{b_{1}=\frac{\vec{a}\circ \vec{b}}{a}=\frac{30}{3\sqrt{5}}=\frac{10\sqrt{5}}{5}=2\sqrt{5}}\)
Polecenie
Wyznacz współrzędne wektora \(\vec{b}_1\). Wybierz, spośród trzech, jedną prawidłowa odpowiedź.
Współrzędne wektora \(\vec{b}_1\) wynoszą \(\vec{b}_1=2\,\hat{i}+4\,\hat{j}\)
Rozwiązanie - etap 2
Długość wektora \(\vec{a}\) wynosi:
\(a=\sqrt{6^2+3^2}=\sqrt{45}=3\sqrt{5}\)
Współrzędne wektora jednostkowego \(\vec{n}_a\) wynoszą:
\(\displaystyle{\vec{n}_{a}=\frac{1}{a}\left ( 6\,\hat{i}+3\,\hat{j} \right )=\frac{1}{3\sqrt{5}}\left ( 6\,\hat{i}+3\,\hat{j} \right )}\)
Współrzędne wektora \(\vec{b}_1\) wynoszą:
\(\displaystyle{\vec{b}_{1}=b_{1}\cdot\vec{n_{a}}=2\sqrt{5}\cdot \frac{1}{3\sqrt{5}}\left ( 6\,\hat{i}+3\,\hat{j} \right )}\)
\(\displaystyle{\vec{b}_{1}=\frac{2}{3}\left ( 6\,\hat{i}+3\,\hat{j} \right )=4\,\hat{i}+2\,\hat{j}}\)
Polecenie
Ostatni etap rozwiązania polega na wyznaczeniu współrzędnych wektora \(\vec{b}_2\). Rozwiąż samodzielnie i sprawdź otrzymany wynik.
Możesz również sprawdzić dwie propozycję rozwiązania
Odpowiedź
Składowe wektora \(\vec{b}\) wyznaczone względem wektora \(\vec{a}\) wynoszą \(\vec{b_{1}}=4\,\hat{i}+2\,\hat{j}\) oraz \(\vec{b_{2}}=-\hat{i}+2\,\hat{j}\)
Rozwiązanie - etap 3
Metoda 1
Rzut prostopadły wektora \(\vec{b}\) na wektor \(\vec{a}\) można wyznaczyć z zależności:
\(\vec{b}=\vec{b_{1}}+\vec{b_{2}}\)
\(\vec{b_{2}}=\vec{b}-\vec{b_{1}}\)
\(\vec{b_{2}}=3\,\hat{i}+4\,\hat{j}-\left(4\,\hat{i}+2\,\hat{j}\right)\)
\(\vec{b_{2}}=-\hat{i}+2\,\hat{j}\)
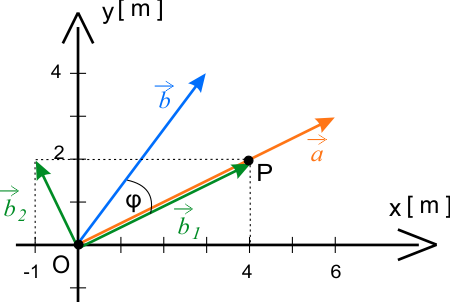
Odpowiedź
Składowe wektora \(\vec{b}\) wyznaczone względem wektora \(\vec{a}\) wynoszą \(\vec{b_{1}}=4\,\hat{i}+2\,\hat{j}\) oraz \(\vec{b_{2}}=-\hat{i}+2\,\hat{j}\).
Rozwiązanie - etap 3
Metoda 2
Metoda druga jest metodą alternatywną. Przedstawia ona inny sposób rozwiązania, który wymaga większej ilości obliczeń.
Do wyznaczenia rzutu prostopadłego wektora \(\vec{b}\) na wektor \(\vec{a}\) można użyć wektora jednostkowego \(\vec{n_{\perp}}\).
Wektor jednostkowy \(\vec{n_{\perp}}\) można zapisać jako:
Mamy więc do rozwiązania układ równań:
Podstawiając \(y\) do pierwszego równania mamy:
Rozwiązaniem układu równań są dwa wektory prostopadłe do wektora \(\vec{a}\). Warunki zadania spełnia wektor skierowany w górę, czyli:
Do wyznaczenia współrzędnych wektora \(\vec{b_{2}}\) potrzebna jest jeszcze długość tego wektora. Wyznaczyć ją można z twierdzenia Pitagorasa:

Odpowiedź
Składowe wektora \(\vec{b}\) wyznaczone względem wektora \(\vec{a}\) wynoszą \(\vec{b_{1}}=4\,\hat{i}+2\,\hat{j}\) oraz \(\vec{b_{2}}=-\hat{i}+2\,\hat{j}\).