Zadanie 1.4.2.3
  1. Kurs obliczeniowy z fizyki
  2. 1. Wektory
  3. 1.4 Iloczyn wektorowy
  4. 1.4.2 Trening
  5. Zadanie 1.4.2.3

 Zadanie 1.4.2.3

Iloczyn wektorowy i prędkość kątowa
Prędkość kątowa obiektu poruszającego się po okręgu wynosi \(\displaystyle{\vec{\omega}=\frac{3}{4}\pi\, \hat{k}\;\mathrm{\frac{rad}{s}}}\). W pewnej chwili czasu wektor wodzący opisujący ruch obiektu wynosi \(\vec{r}=(3\,\hat{i}+4\,\hat{j})\;\mathrm{m}\). Wyznacz wektor prędkości liniowej tego obiektu. Sporządź rysunek.

 Wskazówka teoretyczna

 Wskazówka teoretyczna
Prędkość kątowa \(\vec{\omega}\) i liniowa \(\vec{v}\) w ruchu krzywoliniowym są związane zależnością \(\vec{v}=\vec{\omega}\times\vec{r}\), gdzie \(\vec{r}\) jest wektorem wodzącym.

Zwrot wektora będącego wynikiem iloczynu wektorowego określa kierunek ruchu śruby prawoskrętnej w trakcie nakładania pierwszego z wektorów iloczynu, na drugi. Zmiana kolejności nakładania wektorów oznacza zmianę znaku iloczynu wektorowego.

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- współrzędne wektora prędkości kątowej \(\vec{\omega}=\frac{3}{4}\pi\, \hat{k}\),
- współrzędne wektora wodzącego \(\vec{r}=3\,\hat{i}+4\,\hat{j}\).

Szukane:
- współrzędne wektora prędkości liniowej \(\vec{V}\).

Odpowiedź

Współrzędne wektora prędkości liniowej wynoszą \(\displaystyle{\vec{v}=(-3 \pi\,\hat{i}+2,25\pi\,\hat{j})\;\mathrm{\frac{m}{s}}}\).

Polecenie

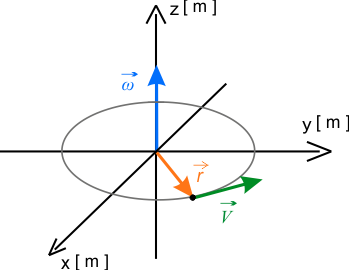
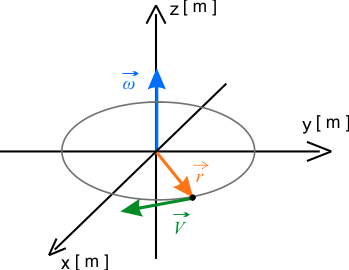
Wybierz jeden z dwóch rysunek, który poprawnie przedstawia sytuacje opisaną w zadaniu.

Wykres 1 z 2
 
Wektory prędkość kątowej i liniowej w kartezjańskim układzie współrzędnych.

Odpowiedź prawidłowa

Wykres 2 z 2

Wektory prędkość kątowej i liniowej w kartezjańskim układzie współrzędnych.

Odpowiedź nieprawidłowa

Polecenie

Wskaż, wśród trzech, jeden prawidłowo wyznaczony wektor prędkości liniowej.

Wybór 1 z 3

\(\displaystyle{\vec{v}=-\frac{3}{4}\pi}\)

Odpowiedź niepraawidłowa

Wybór 2 z 3

\(\displaystyle{\vec{v}=\frac{3}{4} \pi\,\hat{i}+\frac{9}{4}\pi\,\hat{j}}\)

Odpowiedź nieprawidłowa

Wybór 3 z 3

\(\vec{v}=-3 \pi\,\hat{i}+2,25\pi\,\hat{j}\)

Odpowiedź prawidłowa

Rozwiązanie

\(\displaystyle{\vec{v}=\vec{\omega}\times\vec{r}=(0\cdot 0-\frac{3}{4}\pi\cdot4)\hat{i}+(\frac{3}{4}\pi\cdot3-0\cdot0)\hat{j}+(0\cdot4-0\cdot3)\hat{k}}\)
\(\displaystyle{\vec{v}=(-3\pi\,\hat{i}+\frac{9}{4}\pi\,\hat{j})\;\mathrm{\frac{m}{s}}}\)

Odpowiedź

Współrzędne wektora prędkości liniowej wynoszą \(\displaystyle{\vec{v}=(-3 \pi\,\hat{i}+2,25\pi\,\hat{j})\;\mathrm{\frac{m}{s}}}\).