Zadanie 1.4.2.4
  1. Kurs obliczeniowy z fizyki
  2. 1. Wektory
  3. 1.4 Iloczyn wektorowy
  4. 1.4.2 Trening
  5. Zadanie 1.4.2.4

 Zadanie 1.4.2.4

Wektorysław dla odważnych miał zadanie. Czy zerkniesz na nie?
W bezwietrzny dzień Fizaliusz i Wektorysław urządzili zawody strzeleckie. Nad brzegiem Odry ustawili tarczę tak, że strzały leciały w kierunku zachodnim. Wektorysław trafił w sam środek tarczy, a Fizaliusz tuż obok w odległości \(9\,\mathrm{mm}\) od strzały Wektorysława. Fizaliusz stwierdził, że zapomniał o sile Coriolisa, więc gdy przenieśli tarczę i strzelali w kierunku południowym, ich strzały trafiły w ten sam punkt. Fizaliusz stwierdził, że skorygował kurs o \(7\,\mathrm{mm}\). Czy Fizaliusz trafnie ocenił sytuacje? Wykonaj obliczenia przyjmując, że szybkość strzały wynosi \(\displaystyle{v=80\mathrm{\frac{m}{s}}}\), czas przelotu \(\mathrm{t=1,25\;s}\), zaś szerokość geograficzna \(\varphi=51^{\circ}\).
Wektorysław strzela

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Odpowiedź

Podczas strzału z łuku w kierunku zachodnim siła Coriolisa powoduje odchylenie strzały o \(9 \,\mathrm{mm}\), zaś podczas strzelania w kierunku południowym siła ta powoduje odchylenie strzały o \(7 \,\mathrm{mm}\). Fizaliusz trafnie ocenił sytuacje.

Polecenie

Poniżej przedstawione są dane:

- wartość prędkości strzały: \(\displaystyle{v=80\mathrm{\frac{m}{s}}}\),
- czas przelotu: \(\mathrm{t=1,25\;s}\),
- szerokość geograficzna: \(\varphi=51^{\circ}\),
- różnica w położeniu śladów na tarczy po strzale w kierunku zachodnim: \(9\, \mathrm{mm}\).

Wskaż wśród dwóch zestawów szukanych jeden pasujące do treści zadania.

Zestaw 1 z 2

Szukane:

- równanie opisujące tor przelotu strzał.

Odpowiedź nieprawidłowa

Zestaw 1 z 2

Szukane:                            
Odchylenie toru ruchu wynikające z działania siły Coriolisa:
- strzał w kierunku zachodnim: \( \Delta x_{1}\),
- strzał w kierunku południowym: \( \Delta x_{2}\).

Odpowiedź prawidłowa

Polecenie

Wybierz, wśród trzech, najprostszą zależność, którą należy użyć w przypadku strzelania z łuku w stronę zachodnią.

 Wskazówka teoretyczna
Siła Coriolisa - efekt występujący w obracających się układach odniesienia. Siła Coriolisa jest pozorna, występującą jedynie w obracających się układach nieinercjalnych. Dla zewnętrznego obserwatora siła ta nie istnieje.

Siła Coriolisa wyrażana jest wzorem:
\(\vec{F_{c}}=2\,m\,(\vec{v}\times\vec{\omega})\),
gdzie \(m\) oznacza masę ciała posiadającego prędkość liniową \(\vec{v}\), \(\vec{\omega}\) opisuje prędkość kątową układu.

Wybór 1 z 3

\(\vec{F_{c}}=2\,m\,(\vec{v}\times\vec{\omega})\)

Odpowiedź nieprawidłowa

 Wybór 2 z 3

\(F_{c}=2\,m\,v\,\omega\)

Odpowiedź prawidłowa

Wybór 3 z 3

\(F_{c}=2\,m\,v\,\omega\, \sin\alpha\)

Odpowiedź nieprawidłowa

Rozwiązanie - etap 1

Siłę Coriolisa występującą między wektorem prędkości liniowej a kątowej można opisać zależnością:

\(\vec{F_{c}}=2\,m\,(\vec{v}\times\vec{\omega})\)
W sytuacji, w której strzała posyłana jest w kierunku zachodnim, siła Coriolisa skierowana jest prostopadle do Ziemi. Wartość siły wynosi
\(F_{c}=2\,m\,v\,\omega\, \sin{\alpha}\)
Wektory \(\vec{\omega}\) oraz \(\vec{V}\) są prostopadłe do siebie, więc wartość siły Coriolisa można zapisać następująco \(\left (\sin\,{\alpha}=\sin\, 90^{\circ}=1\right )\):
\(F_{c}=2\,m\,v\,\omega\)

Siły działające na strzałę

Siła \(\vec{F_{c}}\) nadaje strzale o masie m przyspieszenie: \(\displaystyle{a=\frac{F_{c}}{m}}\)
Po przyrównaniu dwóch wyrażeń na siłę otrzymujemy:
\(m\cdot a=2\,m\,v\,\omega\)
\(a=2\,v\,\omega\)
Odchylenie toru ruchu strzały można określić z zależności opisującej położenie ciała w ruchu jednostajnie opóźnionym: \(\Delta x_{1} = \frac{1}{2}a\,t^{2}\), gdzie \(a\) jest przyspieszeniem wywołanym przez siłę Coriolisa.

Polecenie

Wskaż, spośród trzech, prawidłową wartość odchylenia toru ruchu strzały przy wystrzale w kierunku zachodnim.

Wybór 1 z 3

\(\mathrm{\Delta x_{1}\approx 10\,mm}\)

odpowiedź nieprawidłowa

Wybór 2 z 3

\(\mathrm{\Delta x_{1}\approx 9\,mm}\)

Odpowiedź prawidłowa

Wybór 3 z 3

\(\mathrm{\Delta x_{1}\approx 8\,mm}\)

Odpowiedź nieprwidłowa

Obliczenia

\(\Delta x_{1} =\frac{1}{2}\cdot 2\cdot v\cdot \omega \cdot t^{2}\)
Wartość prędkości kątowej Ziemi wynosi: \(\displaystyle{\omega = \frac{2\pi}{24\cdot 3600}=7,27\cdot 10^{-5}}\)   \(\displaystyle{ \mathrm{\left[\frac{rad}{s} \right ]}}\)
\(\Delta x_{1} = v\cdot \omega \cdot t^{2}=80\cdot 7,27\cdot 10^{-5} \cdot (1,25)^{2}\)
\(\Delta x_{1} =0,00909\)            \(\displaystyle{\mathrm{\left [ \frac{m}{s}\cdot\frac{rad}{s}\cdot s^2=m \right ]}}\)
\(\Delta x_{1}= 0,00909\,\mathrm{m \approx 9\,mm}\)

Polecenie

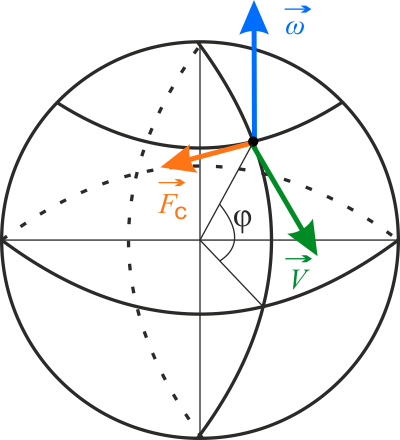
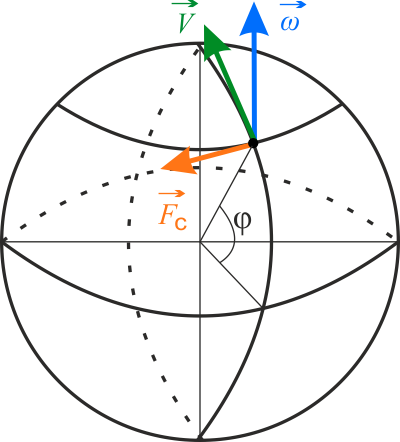
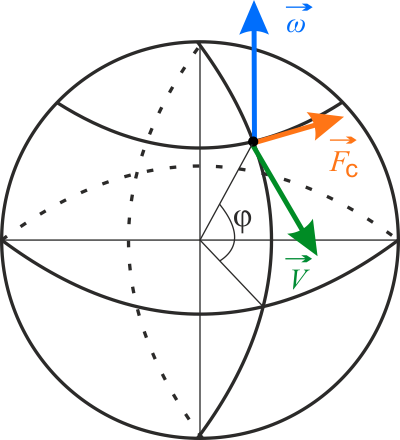
Wybierz, spośród trzech, rysunek, na którym prawidłowo zaznaczone są wektory: prędkość kątowa, prędkość liniowa oraz siła Coriolisa w przypadku, gdy strzały zostały wystrzelone w kierunku południowym.

Wybór 1 z 3

Siły działające na strzałę

Odpowiedź prawidłowa

Wybór 2 z 3

Siły działające na strzałę

Odpowiedź nieprawidłowa

Wybór 3 z 3

Siły działające na strzałę

Odpowiedź nieprawidłowa
Wektor prędkości skierowany jest wzdłuż południka w kierunku bieguna południowego. Z reguły prawej ręki wynika, że po nałożeniu wektora prędkości \(\vec{v}\) na wektor prędkości kątowej \(\vec{\omega}\) przez mniejszy kąt, wektor przedstawiający siłę Coriolisa, skierowany jest na zachód.

Polecenie

Wybierz, spośród trzech zależność, którą należy użyć w przypadku strzelania z łuku w kierunku południa.

Wybór 1 z 3

\(\vec{F_{c}}=m\,(\vec{v}\times\vec{\omega})\)

Odpowiedź nieprawidłowa

Wybór 2 z 3

\(F_{c}=2\,m\,v\,\omega\)

Odpowiedź nieprawidłowa

Wybór 3 z 3

\(F_{c}=2\,m\,v\,\omega \sin{\alpha}\)

Odpowiedź prawidłowa

Rozwiązanie - etap 2

Wartość siły wynosi

\(F_{c}=2\,m\,v\,\omega\, \sin{\alpha}\).

W sytuacji, w której strzała posyłana jest w kierunku południa, siła Coriolisa skierowana jest wzdłuż równoleżnika, w kierunku wschodnim.
Wektory \(\vec{\omega}\) oraz \(\vec{v}\) nie są prostopadłe do siebie, więc siłę Coriolisa należy wyznaczyć z zależności:

\(F_{c}=2\,m\,v\,\omega\, \sin{\alpha}\).

W tym przypadku należy wyznaczyć kąt pomiędzy obydwoma wektorami prędkości. 

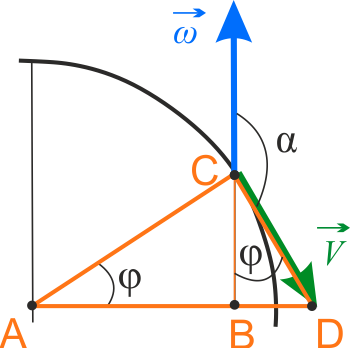
Kąt pomiędzy wektorami prędkości liniowej i kątowej


Na rysunku powyżej widać, że kąty \(\angle CAB \) oraz \(\angle BCD\) maja tą sama wartość. Kąt \(\alpha\) wynosi więc \(\alpha=180^{\circ}-\varphi\). Sinus kata \(\alpha\) wynosi więc \(\sin \alpha=\sin (180^{\circ}-\varphi)=\sin \varphi\).

W tym przypadku przyspieszenie wynosi: \(a= 2\,v\,\omega\,\sin \varphi\). Odchylenie toru ruchu strzały można określić z zależności opisującej położenie ciała w ruchu jednostajnie opóźnionym: \(\Delta x_{1} = \frac{1}{2}a\,t^{2}\), gdzie \(a\) jest przyspieszeniem wywołanym przez siłę Coriolisa.

Polecenie

Wskaż, spośród trzech, prawidłową wartość odchylenia toru ruchu strzały przy wystrzale w kierunku południowym.

Wybór 1 z 3

\(\mathrm{\Delta x_{1}\approx 11\,mm}\)

Odpowiedź nieprawidłowa

Wybór 2 z 3

\(\mathrm{\Delta x_{1}\approx 9\,mm}\)

Odpowiedź nieprawidłowa

Wybór 3 z 3

\(\mathrm{\Delta x_{1}\approx 7\,mm}\)

Odpowiedź prawidłowa

Obliczenia

\(\Delta x_{2} =\frac{1}{2}\cdot 2\cdot v\cdot \omega\cdot \sin\varphi \cdot t^{2}\)
Wartość prędkości kątowej Ziemi wynosi: \(\displaystyle{\omega = \frac{2\pi}{24\cdot 3600}=7,27\cdot 10^{-5}}\)   \(\displaystyle{ \mathrm{\left[\frac{rad}{s} \right ]}}\)
\(\Delta x_{2} = v\cdot \omega \cdot t^{2}=80\cdot 7,27\cdot 10^{-5} \cdot \sin 51^{\circ} \cdot (1,25)^{2}\)
\(\Delta x_{2} =0,007064\)            \(\displaystyle{\mathrm{\left [ \frac{m}{s}\cdot\frac{rad}{s}\cdot s^2=m \right ]}}\)
\(\Delta x_{2}= 0,007064\,\mathrm{m \approx 7\,mm}\)

Odpowiedź

Podczas strzału z łuku w kierunku zachodnim siła Coriolisa powoduje odchylenie strzały o \(9 \mathrm{\,mm}\), zaś podczas strzelania w kierunku południowym siła ta powoduje odchylenie strzały o \(7 \mathrm{\,mm}\). Fizaliusz trafnie ocenił sytuacje.