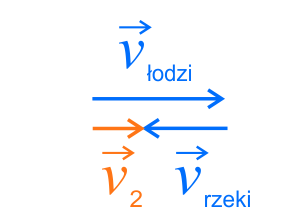Analiza sytuacji

W trakcie analizy sytuacji przedstawionej w zadaniu, ważne jest, aby pamiętać, że prędkość jest wielkością wektorową. Prędkość łodzi będzie zależała od kierunku jej poruszania się, szybkości i zwrotu względem kierunku prądu rzeki. Na prędkość łodzi mają więc wpływ dwie wielkości:

gdzie \(\vec{v}_{rzeki}\) określa prędkość nurtu rzeki zaś przez \(\vec{v}_{łodzi}\) oznaczono prędkość łodzi jaką pozwala osiągnąć jej silnik. Wartość \(\vec{v}\) oznacza prędkość wypadkową.

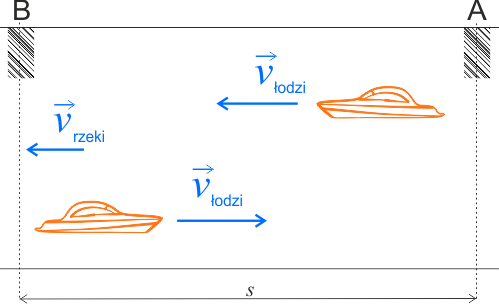
W treści zadania przedstawiono dwie sytuacje, w których łódź porusza się w przeciwnych kierunkach. Te dwie sytuacje należy przeanalizować osobno.

1. Łódź płynie z prądem rzeki.
 Objaśnienie  Łódź płynąca z prądem rzeki, z przystani \(A\) do \(B\), porusza się z prędkością wypadkową \(\vec{v_1}\). Wektory prędkości rzeki i łodzi są zwrócone w tą samą stronę. Można więc zapisać równanie w postaci wektorowej: 

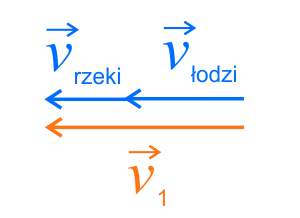
2. Łódź płynie pod prąd rzeki.
 Objaśnienie  Łódź płynąca pod prąd rzeki, z przystani \(B\) do \(A\), porusza się z prędkością wypadkową \(\vec{v_2}\). Tym razem analizowane wektory skierowane są przeciwnie. Można więc zapisać równanie w postaci wektorowej: 
3. Łódź spływa z wyłączonym silnikiem.
 Objaśnienie  Z otrzymanych równań można wyznaczyć szybkość rzeki. Łódź, spływając z wyłączonym silnikiem, porusza się z prądem rzeki, czyli musimy obliczyć czas, jaki potrzebuje rzeka, na przebycie drogi pomiędzy przystaniami. Dryfująca łódź porusza się ruchem jednostajnym, zatem szukany w zadaniu czas \(t\) można obliczyć, korzystając z zależności dla ruchu jednostajnego: 

Rozwiązanie

Uzyskane równania:

Z otrzymanego zestawu równań otrzymujemy kolejno:

Równanie (1) oraz (2) odejmujemy stronami:
 Przekształcenia  \[\eqalign{v_{łodzi}-v_{łodzi}+v_{rzeki}+v_{rzeki} &=\frac{S}{t_1}-\frac{S}{t_2} \\ 2\,v_{rzeki} &=\frac{S}{t_1}-\frac{S}{t_2} \\ 2v_{rzeki} &=\frac{s\,t_2}{t_1t_2}-\frac{s\,t_1}{t_1t_2} \\ 2v_{rzeki} &=\frac{S\,t_2-S\,t_1}{t_1t_2}}\] 

Otrzymaną wartość \(v_{\mathrm{rzeki}}\) podstawiamy do wzoru (3) \(\displaystyle{t=\frac{S}{v_{\mathrm{rzeki}}}}\)
 Przekształcenia  \[\eqalign{t &=\frac{S}{\large{\frac{S}{2}}\cdot \frac{t_2-t_1}{t_1t_2}} \\t &=\frac{2}{\frac{t_2-t_1}{t_1t_2}}=2\cdot \frac{t_1t_2}{t_2-t_1}}\]  Po wyprowadzeniu wzoru można podstawić wielkości liczbowe.