Zadanie 2.1.1.4
Wskazówka teoretyczna
\[v=v_0+at\]
\(v_0\) - wartość prędkości początkowej,
\(a\) - wartość przyspieszenia \(a=const\).
Droga \(S\) przebyta przez ciało w ruchu jednostajnie przyspieszonym po czasie \(t\):
\[\displaystyle{S=S_0+v_0t+\frac{1}{2}at^2}\]
\(S_0\) - droga początkowa w chwili \(t=0\),
\(v_0\) - wartość prędkości początkowej,
\(a\) - wartość przyspieszenia \(a=const\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- czas ruchu pojazdów \(t\),
- pierwszy etap ruchu pojazdu \(A\): \(\displaystyle{t_{1A}=\frac{1}{2}t}\), \(a_{1A}=a\),
- drugi etap ruchu pojazdu \(A\): \(\displaystyle{t_{2A}=\frac{1}{2}t}\), \(a_{2A}=3a\),
- pierwszy etap ruchu pojazdu \(B\): \(\displaystyle{t_{1B}=\frac{1}{2}t}\), \(a_{1B}=3a\),
- drugi etap ruchu pojazdu \(B\): \(\displaystyle{t_{2B}=\frac{1}{2}t}\), \(a_{2B}=a\),
Szukane:
- stosunek dróg przebytych przez pojazd \(A\) oraz \(B\): \(\displaystyle{\frac{S_B}{S_A}}\),
- wykres zależności prędkości w funkcji czasu.
Rozwiązanie - pojazd A
Czas jazdy nie jest znany. Wiadomo jedynie, że pojazdy poruszały się tak samo długo. Oznaczmy ten czas jako \(t\).
Przebytą drogę pojazdu \(A\) można zapisać następująco:
\(S_A=S_{1A}+S_{2A}\),
gdzie indeksy \(1A\) oraz \(2A\) oznaczają odpowiednio pierwszą i druga połowę czasu.
Pierwszy etap ruchu pojazdu \(A\) - prędkość oraz droga początkowa wynosi zero.
\(\displaystyle{S_{1A}=\frac{a_{1A}\,t_{1A}^2}{2}=\frac{a\,(\frac{t}{2})^2}{2}=\frac{at^2}{8}}\)
Drugi etap ruchu pojazdu \(A\)
\(\displaystyle{S_{2A}=v_A\,t_{2A}+\frac{a_{2A}\,t_{2A}^2}{2}=v_A\,\frac{t}{2}+\frac{3a\,(\frac{t}{2})^2}{2}}\)
\(\displaystyle{S_{2A}=\frac{1}{2}v_A\,t+\frac{3a\,t^2}{8}}\)
\(v_A\) jest prędkością jaka osiągną pojazd \(A\) po połowie czasu. Prędkość ta wynosi:
\(\displaystyle{v_A=a_{1A}\,t_{1A}=a\,\frac{t}{2}=\frac{1}{2}a\,t}\)
Droga w drugim etapie ruchu wynosi:
\(\displaystyle{S_{2A}=\frac{1}{2}v_A\,t+\frac{3a\,t^2}{8}=\frac{1}{2}\cdot\frac{1}{2}at\cdot\,t+\frac{3a\,t^2}{8}}\)
\(\displaystyle{S_{2A}=\frac{2\cdot at^2}{2\cdot 4}+\frac{3a\,t^2}{8}=\frac{5a\,t^2}{8}}\)
Droga przebyta przez pojazd \(A\) wynosi:
\(\displaystyle{S_A=S_{1A}+S_{2A}=\frac{at^2}{8}+\frac{5a\,t^2}{8}=\frac{6a\,t^2}{8}}\)
\(\displaystyle{S_A=\frac{3}{4}at^2}\)
Rozwiązanie - pojazd B
Czas jazdy nie jest znany. Wiadomo jedynie, że pojazdy poruszały się tak samo długo. Oznaczmy ten czas jako \(t\).
Przebytą drogę pojazdu \(B\) można zapisać następująco:
\(S_B=S_{1B}+S_{2B}\),
gdzie indeksy \(1B\) oraz \(2B\) oznaczają odpowiednio pierwszą i druga połowę czasu.
Pierwszy etap ruchu pojazdu \(B\) - prędkość oraz droga początkowa wynosi zero.
\(\displaystyle{S_{1B}=\frac{a_{1B}\,t_{1B}^2}{2}=\frac{3a\,(\frac{t}{2})^2}{2}=\frac{3at^2}{8}}\)
Drugi etap ruchu pojazdu \(B\)
\(\displaystyle{S_{2B}=v_B\,t_{2B}+\frac{a_{2B}\,t_{2B}^2}{2}=v_B\,\frac{t}{2}+\frac{a\,(\frac{t}{2})^2}{2}}\)
\(\displaystyle{S_{2B}=\frac{1}{2}v_B\,t+\frac{a\,t^2}{8}}\)
\(v_B\) jest prędkością jaka osiągną pojazd \(B\) po połowie czasu. Prędkość ta wynosi:
\(\displaystyle{v_B=a_{1B}\,t_{1B}=3a\,\frac{t}{2}=\frac{3}{2}a\,t}\)
Droga w drugim etapie ruchu wynosi:
\(\displaystyle{S_{2B}=\frac{1}{2}v_B\,t+\frac{a\,t^2}{8}=\frac{1}{2}\cdot\frac{3}{2}at\cdot\,t+\frac{a\,t^2}{8}}\)
\(\displaystyle{S_{2B}=\frac{2\cdot 3at^2}{2\cdot 4}+\frac{a\,t^2}{8}=\frac{7a\,t^2}{8}}\)
Droga przebyta przez pojazd \(B\) wynosi:
\(\displaystyle{S_B=S_{1B}+S_{2B}=\frac{3at^2}{8}+\frac{7a\,t^2}{8}=\frac{10a\,t^2}{8}}\)
\(\displaystyle{S_B=\frac{5}{4}at^2}\)
Rozwiązanie
Z obliczeń wynika, że droga przebyta przez drugie ciało jest większa.
Stosunek przebytych dróg wynosi:
\(\displaystyle{\frac{S_B}{S_A}=\frac{\frac{5}{4}at^2}{\frac{3}{4}at^2}=\frac{5}{4}\cdot \frac{4}{3}=\frac{5}{3}}\)
Informacja
Kolejne etapy rysowania wykresu możesz zobaczyć klikając w przyciski umieszczone pod wykresem.
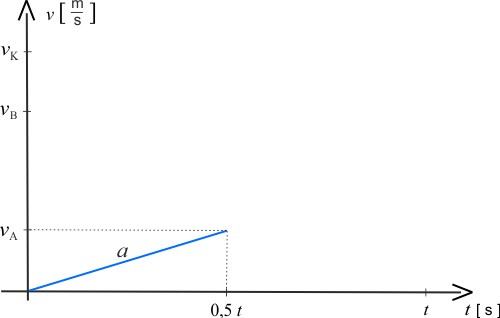
Pojazd \(A\) pierwszą połowę czasu porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem \(a\). W czasie \(t=0,5\,t\) osiągnie prędkość \(v_A\).
Wartość prędkości w czasie zmienia się w sposób liniowy - ruch jednostajny.
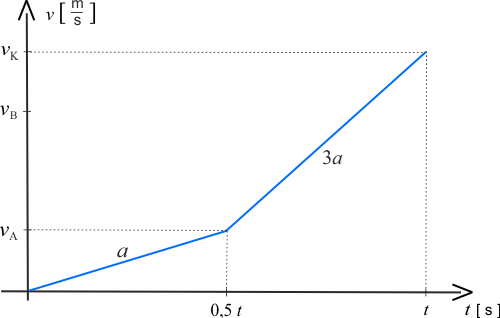
Pojazd \(A\) drugą połowę czasu porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem \(3a\). W czasie \(t=0,5\,t\) osiągnie prędkość końcową \(v_K\).
Wartość prędkości w czasie zmienia się w sposób liniowy - ruch jednostajny.
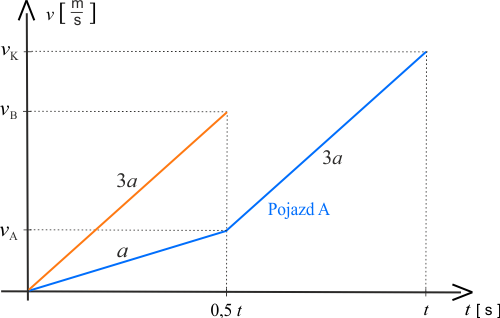
Pojazd \(B\) pierwszą połowę czasu porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem \(3a\). W czasie \(t=0,5\,t\) osiągnie prędkość \(v_B\).
Wartość prędkości w czasie zmienia się w sposób liniowy - ruch jednostajny.
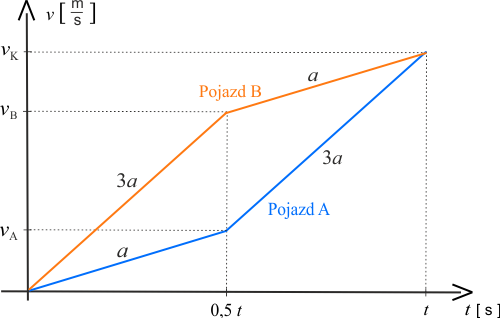
Pojazd \(B\) drugą połowę czasu porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem \(a\). W czasie \(t=0,5\,t\) osiągnie prędkość końcową \(v_K\).
Wartość prędkości w czasie zmienia się w sposób liniowy - ruch jednostajny.
Rozwiązanie
Punktem wyjściowym dla drugiej metody, jest sporządzenie wykresu.
Etap 1
Dwa pojazdy zmieniają przyspieszenie w połowie czasu jazdy. Na wykresie należy zaznaczyć prędkość jaką jeden i drugi osiągnie po tym czasie. Pojazd \(A\) jedzie z przyspieszeniem \(a\) trzykrotnie mniejszym niż pojazd \(B\), więc prędkość pojazdu \(A\) będzie mniejsza od prędkości pojazdu \(B\).
Prędkość \(v_A\), jaką pojazd \(A\) osiągnie po połowie czasu wynosi:
Prędkość \(v_B\), jaką pojazd \(B\) osiągnie po połowie czasu wynosi:
Wartość prędkości czyli szybkość \(v_B\) jest trzykrotnie większa od wartości prędkości \(v_A\).
Poniżej przedstawiono wykresy prędkości w ruchu jednostajnie przyspieszonym, dla dwóch pojazdów poruszających się w pierwszej połowie czasu jazdy.
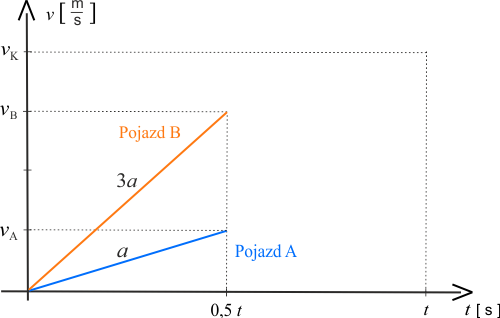
Etap 2
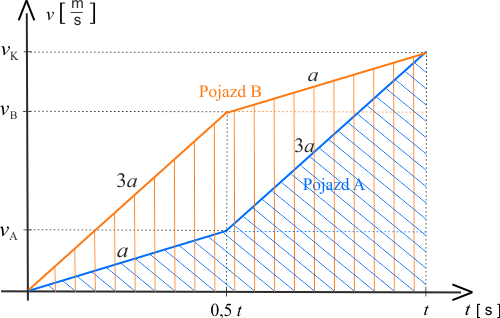
Po zmianie przyspieszenia przez oba pojazdy po połowie czasu, wartość prędkości końcowej \(v_K\) obu będzie taka sama:
Na wykresie poniżej przedstawiono wykresy prędkości w ruchu jednostajnie przyspieszonym dla dwóch pojazdów.

Pola pod krzywymi opisującymi ruch pojazdów są, co do wartości równe przebytym drogom, można więc obliczyć te pola i policzyć ich stosunek. Poniżej przedstawiono wykres z zaznaczonymi polami: \(P_A\) równe przebytej drodze przez pojazd \(A\), zaznaczone niebieskimi pochylonymi kreskami oraz \(P_B\) równe przebytej drodze przez pojazd \(B\) zaznaczone niebieskimi pionowymi kreskami.
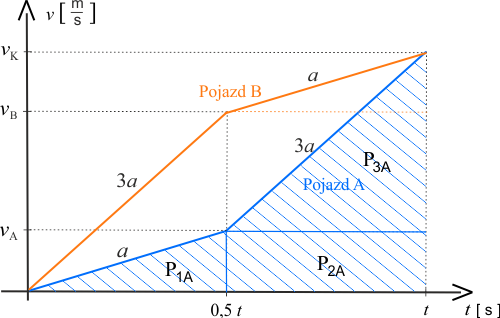
Droga \(S_A\)
Pole pod wykresem dla pojazdu \(A\) wynosi:
\(\displaystyle{S_A=P_{1A}+P_{2A}+P_{3A}}\)
\(\displaystyle{S_A=\frac{1}{2}\cdot \frac{t}{2}\cdot v_A+v_A \cdot \frac{t}{2}+\frac{1}{2}\cdot \frac{t}{2}\left ( v_K-v_A\right )}\)
\(\displaystyle{S_A=\frac{t}{4}\cdot \frac{1}{2}at+\frac{1}{2}at \cdot \frac{t}{2}+\frac{t}{4} \left ( 2at-\frac{1}{2}at \right )}\)
\(\displaystyle{S_A=\frac{at^2}{8}+\frac{at^2}{4}+\frac{t}{4}\cdot \frac{3}{2}at }\)
\(\displaystyle{S_A=\frac{at^2}{8}+\frac{2at^2}{8}+\frac{3at^2}{8}=\frac{6}{8}at^2}\)
\(\displaystyle{S_A=\frac{3}{4}at^2}\)
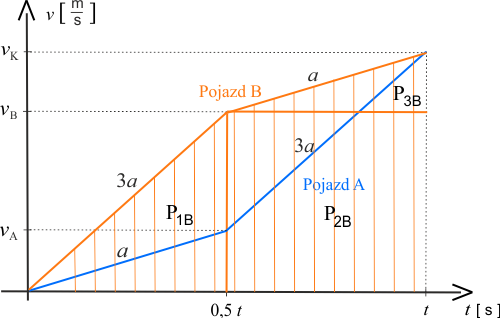
Droga \(S_B\)
Pole pod wykresem dla pojazdu \(B\) wynosi:
\(\displaystyle{S_B=P_{1B}+P_{2B}+P_{3B}}\)
\(\displaystyle{S_B=\frac{1}{2}\cdot \frac{t}{2}\cdot v_B+v_B \cdot \frac{t}{2}+\frac{1}{2}\cdot \frac{t}{2}\left ( v_K-v_B\right )}\)
\(\displaystyle{S_B=\frac{t}{4}\cdot \frac{3}{2}at+\frac{3}{2}at \cdot \frac{t}{2}+\frac{t}{4} \left ( 2at-\frac{3}{2}at \right )}\)
\(\displaystyle{S_A=\frac{3at^2}{8}+\frac{3at^2}{4}+\frac{t}{4}\cdot \frac{1}{2}at }\)
\(\displaystyle{S_A=\frac{3at^2}{8}+\frac{6at^2}{8}+\frac{at^2}{8}=\frac{10}{8}at^2}\)
\(\displaystyle{S_B=\frac{5}{4}at^2}\)
Rozwiązanie
Z obliczeń wynika, że droga przebyta przez drugie ciało jest większa.
Stosunek przebytych drug wynosi:
\(\displaystyle{\frac{S_B}{S_A}=\frac{\frac{5}{4}at^2}{\frac{3}{4}at^2}=\frac{5}{4}\cdot \frac{4}{3}=\frac{5}{3}}\)
